Alcance y restricciones de la lógica y los sistemas axiomáticos en la teoría de la utilidad esperada

Luciano Milillo

Finally, one economist concluded the discussion with the following dictum: “Look,” he said with conviction, “either reasoning is rational or it’s psychological”.

[Por último, un economista concluyó el debate con la siguiente sentencia: “Miren”, dijo convencido, “o el razonamiento es racional o es psicológico”].

   

Gerd Gigerenzer, Adaptative thinking

Introducción

Suele suceder que entre los estudiantes de los primeros cursos de lógica se repite una y otra vez una pregunta como si fuera un mantra: ¿para qué me sirve esta disciplina? Generalmente aparece cuando se enfoca a la materia desde un punto de vista extremadamente formal y deductivista. Es difícil ver la relación entre las conectivas de la lógica proposicional o los cuantificadores, ni hablar de la deducción natural, con la argumentación de la vida cotidiana o lo persuasivos o no que puedan ser determinados argumentos.

En este capítulo no pretendo hacer una defensa de la lógica formal, de la deducción o una crítica hacia ella. La propuesta será mostrar la importancia de los sistemas formales para poder estudiar y entender una disciplina pero, asimismo, mostrar sus límites. De esta manera, intentaré señalar las virtudes (y los defectos) que la lógica deductiva nos puede brindar, a partir de las ciencias económicas y la psicología. Con esto quiero decir que analizaré qué es un sistema axiomático y cómo ciertas reglas de deducción nos permiten desarrollar una teoría, en este caso, tanto económica como psicológica. No obstante, esta manera de abordar estas disciplinas también da lugar a paradojas y problemas con las decisiones de los humanos del mundo real.

Como sospechará el lector, la intersección entre la psicología, la economía y la lógica es la teoría de la decisión racional, específicamente la teoría de la utilidad. Esto es así porque el concepto de utilidad nos permitirá apreciar el valor de la deducción de los sistemas axiomáticos pero también porque la psicología experimental mostrará los límites de estos.

De esta manera, comenzaré exponiendo brevemente qué es la lógica y su función en los sistemas axiomáticos. Luego, expondré el surgimiento del concepto de utilidad a partir de la paradoja de San Petersburgo para pasar a la deducción del teorema de la utilidad esperada desde el sistema axiomático de von Neumann y Morgenstern (1953). Por último, comentaré un límite que encontró la psicología experimental a la avanzada racionalista en economía y las paradojas propias de los postulados axiomáticos. En definitiva, concluiré que, o bien la teoría de la utilidad esperada necesita algún tipo de revisión, o deberemos aceptar que los seres humanos caen continuamente en actos y decisiones irracionales.

Lógica y sistemas axiomáticos

No hay dudas de que la lógica tiene que ver con las inferencias. Es decir, esta disciplina nos muestra cuál es una buena inferencia y cuál no, por tanto, es necesario que determine cuáles son esas reglas que permiten extraer una conclusión de un conjunto de premisas. Cuando existe necesidad en ese proceso de inferencia es que podemos hablar de deducción. Y, es por eso, que la deducción es clave para cualquier disciplina porque permite derivar proposiciones a partir de otras ya existentes asegurando la transmisión de la verdad.

Suele criticársele a esta disciplina, de manera muy superficial, que las cadenas de razonamientos deductivos no aportan información nueva y, por tanto, no son relevantes para la ampliación de información. Sin embargo, es interesante recuperar la distinción que alguna vez hizo Hintikka en “¿Qué es la lógica?” (2007). Al decir que la deducción no aporta información nueva, en realidad, lo que habría que aclarar es que no agrega información nueva “de profundidad” pero sí de “superficie” (Hintikka y Sandu, 2007, p. 17). Si se plantea a la lógica como un camino de deducciones que no aportan información novedosa entonces se convierte en una disciplina poco estimulante. Sin embargo, sí aporta datos nuevos puesto que la información de superficie puede ir aumentando hasta mostrar la totalidad de la información de profundidad que en principio nos está vedada. Desde esta perspectiva, la información de superficie puede considerarse como el conjunto de conclusiones inmediatas accesibles a partir de premisas dadas, mientras que la información de profundidad implica un análisis más elaborado que revela consecuencias no triviales del sistema deductivo.

En línea con lo anterior, es este valor de la lógica deductiva el que capitaliza el método axiomático. Éste determina cuáles son las verdades fundamentales e intuitivas de un campo que se quiera estudiar para, a partir de ellas, deducir otras proposiciones, conocidas como teoremas. Un caso bien conocido es la geometría de Euclides pero no es sino hasta finales del siglo XIX y principios del XX cuando el método axiomático cobra un auge significativo gracias a David Hilbert. La matemática fue la pionera en este mecanismo para estudiar estructuras determinadas pero luego se expandió a otros campos del conocimiento. La ventaja frente al método experimental, por ejemplo, es que no se necesita un laboratorio ni recolección de datos para investigar.

La lógica cumple una función crucial porque es necesaria como requisito fundamental para que pueda existir un sistema axiomático. Entre los diferentes requerimientos que se deben cumplir para desarrollar un sistema de estas características, hay dos que nos llevan directamente a la lógica: todos los teoremas deben ser consecuencia lógica de sus axiomas y, también, que esos teoremas no pueden agregar nueva información (Hintikka, 2009). Sin embargo, ya sabemos lo que esto significa: no pueden adicionar información de profundidad pero sí de superficie.

De hecho, veremos en el apartado 4.b) lo importante que es la deducción en los sistemas axiomáticos porque los teoremas no son para nada intuitivos, es decir, cuando se analiza a simple vista los axiomas no pueden captarse sin más los teoremas.

A partir de aquí, me concentraré en temas propios de la economía y la psicología. La lógica es nuestro punto de partida pero también será nuestro punto de llegada. Si es una disciplina fundamental para desarrollar la teoría de la decisión racional, cerraremos el capítulo dándonos cuenta de sus limitaciones.

Ahora bien, ¿por qué es necesario un sistema axiomático en economía? La razón de ello hay que buscarla en uno de los conceptos fundamentales de la teoría económica pero que indefectiblemente nos remitirá al campo de la psicología: la noción de utilidad. Término que resulta familiar para cualquiera que se encuentre transitando una carrera en Filosofía pero, así como cualquier término relevante en esta disciplina, no es sencillo de definir. La historia del concepto es compleja pero intentaré revisar algunas cuestiones relevantes para este capítulo. Por ello, comenzaré con un punto de partida habitual dentro de la lógica: las paradojas.

La noción de utilidad en la búsqueda de resolución de paradojas

En lógica las paradojas implican alguna suerte de contradicción. Sin embargo, cuando en economía o matemática se utiliza este término no implica estrictamente problemas de este tipo pero sí se refiere a callejones sin salida o situaciones en las que un agente racional actúa de diferentes maneras frente al mismo tipo de decisión.

Cuando una persona debe tomar una decisión puede hacerlo en diferentes contextos. Puede tener certeza de lo que va a suceder si define tal o cual curso de acción, o puede ignorar cómo resultarán sus actos porque no sabe con exactitud cómo se presentará el estado de cosas. Puede parecer complejo pero es muy sencillo: si uno sabe las probabilidades de los posibles resultados decimos que toma su decisión en contexto de riesgo pero si no hay manera de saber las probabilidades decimos que actúa bajo incertidumbre.

Esta distinción es importante porque distingue diferentes modelos para la toma de decisiones. Para nuestro análisis en particular, necesitaremos adentrarnos en el mundo de las decisiones bajo riesgo. Por ejemplo, una aseguradora puede calcular cuál es la probabilidad de que una persona con cierta edad y género tenga un siniestro o definir si hacer planes al aire libre el fin de semana en base a las probabilidades del pronóstico. Habitualmente se utilizan los juegos de azar como paradigma para el análisis de la toma de decisiones bajo riesgo porque tienen pocos elementos para analizar: un juego de dados, una ruleta, etc.

Teniendo esto presente pensemos en el siguiente juego de apuestas: un crupier te invita a apostar sobre el lanzamiento de una moneda. El juego propuesto consiste en lanzarla repetidamente hasta que salga cara por primera vez. Si la primera cara aparece en la n-ésima tirada, el jugador recibe 2ⁿ unidades monetarias. Por ejemplo, si sale cara en la primera tirada entonces el jugador recibe 2¹ = $2 o en la cuarta 2⁴ = $16. ¿Cuánto estarías dispuesto a pagar para jugar a este juego? Una estrategia para resolver esta decisión bajo riesgo es calcular su valor esperado. Por ejemplo, si tuviese que jugar a elegir entre las dos manos de un crupier que me está escondiendo entre $3 y $7, debería calcular el valor esperado para saber cuánto debería pagar para jugar al juego. Las chances que tengo son ½ de obtener $3 y ½ de obtener $7. Así, en los inicios de la teoría de juegos se estipuló que el valor esperado de este juego era ½ x $3 + ½ x $7 = $5. Este es el monto que debería pagar para entrar al juego. La fórmula es:

VE = p₁. v₁ + p₂. v₂ + … + p_n .v_n

Donde p es la probabilidad y v el dinero que se juega con esa probabilidad.

Ahora bien, volvamos al primero de los juegos. Si utilizamos esta misma estrategia podemos ver que las probabilidades de obtener cara en las subsiguientes tiradas de la moneda van disminuyendo. En la primera tirada tenemos ½ de chances de sacar cara, en la segunda ¼, en la tercera ⅛, y así sucesivamente. De esta manera:

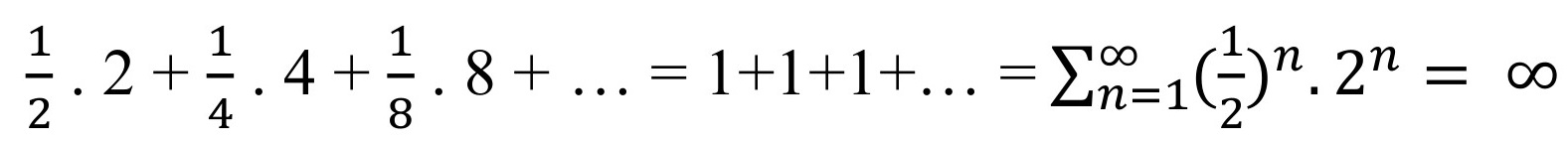
Esta cuenta y subsiguiente fórmula^[1] nos están señalando un problema: el valor esperado del juego es infinito, o lo que es lo mismo, uno debería estar dispuesto a pagar todo lo que tiene para jugar el juego, lo que a todas luces sería inaceptable. Este problema se lo bautizó como la paradoja de San Petersburgo, dado que en esa ciudad impartía sus clases Daniel Bernoulli (1700-82). Este matemático suizo fue el creador de la resolución más famosa de la paradoja, al crear precisamente la teoría de la utilidad esperada, aunque no precisamente con ese nombre.

El problema que encuentra Bernoulli en el juego es que no puede medirse objetivamente el valor que cada persona le asigna a la riqueza. Al introducir esta faceta psicológica al cálculo de la recompensa que brindaba el juego, se vuelve necesaria una modificación en cómo se interpreta ese valor. No es lo mismo $10000 para alguien que no tiene nada para alguien que es millonario. De esta manera, el valor no puede ser objetivo, ni medido estrictamente en términos monetarios. Es necesario incorporar el valor subjetivo de algo o su utilidad^[2]. De esta manera, en la vieja fórmula de valor esperado lo que se debe modificar es ese valor objetivo por el de utilidad.

Ahora bien, el siguiente paso de Bernoulli fue identificar una relación plausible entre una cantidad de dinero x y el beneficio y asociado a ella. Su argumento fue que, al menos en general, el incremento del beneficio y que una persona con una riqueza α obtiene a partir de un aumento x de su riqueza es directamente proporcional a x e inversamente proporcional a α. Esto implica que el beneficio total y que una persona con una riqueza inicial α obtiene de una ganancia monetaria x está dado por el logaritmo natural de (α+x), es decir:

y = ln(α+x)

La función logarítmica es importante porque muestra, en definitiva, la utilidad marginal decreciente, es decir, el beneficio del dinero, en este caso, aumenta pero cada vez con menor intensidad. En una gráfica sería:

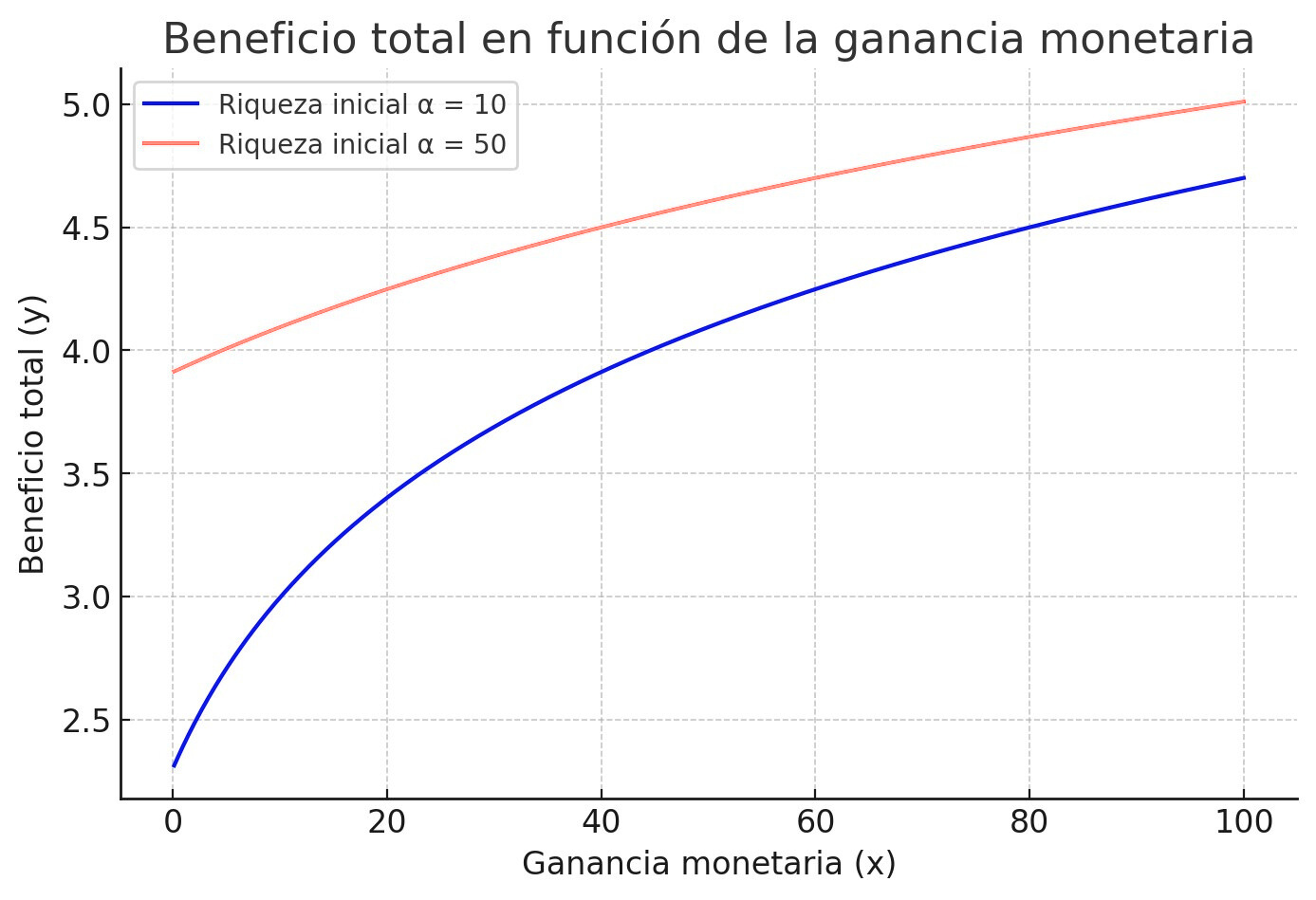
Figura 1. Función de utilidad desde riquezas iniciales diversas.

Esta tabla es ilustrativa de cómo la utilidad no es ya sinónimo de ganancia monetaria. Vemos que a medida que aumentan las ganancias, su utilidad también aumenta pero de manera decreciente. Moscati (2023) reconstruye de manera simplificada las ecuaciones que representan la solución de la paradoja por parte de Bernoulli^[3]. Por ejemplo, si aplicamos la nueva fórmula ya no ponderamos la probabilidad del evento por su valor monetario, sino por su utilidad. Así, veremos que para alguien cuya riqueza inicial es de $1000 el juego no valdría ni $7.

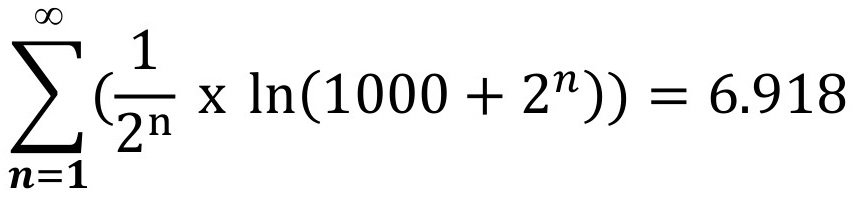
Nuevamente, es una versión simplificada de la fórmula, pero el objetivo es mostrar el tipo de curva que genera en una gráfica.

Más allá de la discusión que pueda suscitar la elección de la función logarítmica para representar, en definitiva, un estado mental subjetivo, conceptualmente la clave está en introducir la noción de utilidad (beneficio en la tabla). Ya no analizamos los números objetivos de dinero sino su valor subjetivo. De esta manera, ya sea una función logarítmica o alguna otra, lo esencial es que demuestre ser creciente y cóncava.

La nueva fórmula pero ahora de utilidad esperada nos queda:

UE = p₁. u₁ + p₂. u₂ + … + p_n.u_n

¿Por qué maximizar la utilidad esperada?

a) El largo plazo

Existen dos caminos para defender por qué es racional maximizar la utilidad esperada en decisiones bajo riesgo. A decir verdad, es el concepto más desarrollado en la teoría de decisiones pero su fundamentación no llega verdaderamente sino hacia mediados del siglo XX. Este camino es la axiomatización, sin embargo, existe otro argumento que explica por qué es una buena herramienta para tomar decisiones.

Las probabilidades de un evento siempre indican cómo se manifiesta dicho evento en el largo plazo. De esta manera, el argumento explota la noción de grandes números. Este teorema matemático establece que cualquier individuo que busque maximizar su utilidad esperada tendrá mejores resultados a largo plazo. Si un experimento aleatorio, como el lanzamiento de un dado o una moneda, se repite n veces y cada intento tiene una probabilidad p de obtener un resultado específico, entonces la probabilidad de que la proporción de esos resultados se desvíe de p por más de una pequeña cantidad disminuye hasta acercarse a cero a medida que n tiende a infinito.

Un ejemplo podría ser el siguiente: imagina que te ofrecen 1 unidad de utilidad con certeza o la opción de participar en un juego de cartas. En este juego, puedes ganar 8 unidades con una probabilidad de 0.25 o no ganar nada con una probabilidad de 0.75. La utilidad esperada de elegir el juego de cartas es 2, lo que es más que 1. De aquí que sea mejor jugar, más allá de que esta vez pierdas. Esto es así, porque la ley de los grandes números lo que nos dice es que si jugáramos una y otra vez nos acercaríamos a la probabilidad indicada.

“En el largo plazo estamos todos muertos”, afirmó Keynes (1992, p. 95). Esto ilustra que una persona no va a estar sometida a la misma decisión una y otra vez, por lo tanto, aplicar esa ley no tiene mucho sentido. Asimismo, existe lo que en matemática se conoce como la ruina del apostador. Una aplicación sencilla de este teorema puede verse en la famosa estrategia de ruleta martingala que consiste en apostar nuevamente duplicando la cantidad que se ha perdido. Por ejemplo, si pierdo dos fichas al rojo vuelvo a apostar al color en la próxima tirada, esperando recuperar lo perdido y ganar algo, asumiendo que la probabilidad de que salga ese color es cercana a 0.5, dependiendo el tipo de ruleta. En el largo plazo tendría sentido pero el asunto es que el capital inicial es finito, por lo que podría perder todo en muy pocas tiradas, porque la apuesta se incrementa al doble de lo anterior en cada tirada. El argumento de la ley de los grandes números tendría sentido si nuestro capital inicial fuera infinito, lo que es una asunción poco realista.

De esta manera, es necesario otro tipo de fundamentación que permita derivar la maximización de la utilidad esperada independientemente de lo que pueda pasar en el largo plazo. Aquí, retomamos lo iniciado en el capítulo, necesitamos un sistema axiomático que fundamente este modelo de toma de decisiones o lo que es lo mismo, un conjunto de verdades intuitivas que permitan derivar un teorema sobre la utilidad esperada.

b) UE de von Neumann y Morgenstern

Habíamos establecido que un sistema axiomático partía desde ciertos postulados indemostrables para luego, a partir de algunas reglas de deducción, derivar teoremas. Esto es precisamente lo que Oskar Morgenstern (1902-77) y John von Neumann (1903-57) realizaron en su obra Theory of games and economic behavior de 1944 con la teoría de la utilidad esperada. En esencia, demostraron que quien toma decisiones bajo riesgo elegirá la opción arriesgada con la expectativa matemática más alta de una función de utilidad cardinal, siempre y cuando sus preferencias entre ciertas opciones cumplan con los axiomas estipulados.

Un elemento que hay que tener presente para desarrollar la teoría de estos autores es el concepto de lotería. Las loterías son las opciones riesgosas sobre las que un agente racional debe elegir. Una nota importante es que un premio con 100% de probabilidad, también será llamado una lotería. Asimismo, el agente puede determinar una relación binaria entre las loterías, indicando cuál prefiere o si le son indiferentes. Así, una preferencia es una relación binaria que se indica con el símbolo ≽. Así, L₁ ≽ L₂ significa que el agente prefiere L₁ sobre L₂ o que le son indiferentes. La preferencia estricta de L₁ sobre L₂ quedaría representada como L₁ ≻ L₂. Como condición de asimetría (Peterson, 2009, p. 99) no puede ser cierto que L₁ ≻ L₂ y L₂ ≻ L₁.

Una aclaración más. Si A y B son loterías, también lo es la perspectiva de obtener A con una probabilidad p y B con una probabilidad de 1-p. Para simplificar, esa situación se representará como ApB.

Habiendo aclarado algunas cuestiones de formalización podemos enumerar los axiomas que establecieron estos autores para estas relaciones de preferencia.

vNM 1: (Completitud) A ≻ B o A ~ B o B ≻ A

La completitud determina que el agente puede determinar las preferencias haciendo un ranking de las loterías desde la primera a la última. Puede preferir, en una relación binaria, una lotería sobre otra o ser indiferente entre ambas. Se asume, por un lado, que el agente conoce todas las alternativas y, por otro, que el agente no puede quedar indeciso frente a ninguna alternativa.

vNM 2: (Transitividad) Si A ≻ B y B ≻ C entonces A ≻ C

  

vNM 3: (Independencia) A ≻ B si y solo si ApC ≻ BpC

Intuitivamente, el axioma de independencia pide que la clasificación de preferencias entre dos loterías no dependa de las partes que ellas tienen en común, sino solo de las partes que las distinguen. De manera más precisa, el axioma establece que, para cualesquiera tres loterías L₁, L₂ y L₃, si el agente prefiere la lotería L₁ a la lotería L₂, entonces también debería preferir la lotería compuesta que otorga L₁ con probabilidad p y L₃ con probabilidad (1 – p), a la lotería compuesta que otorga L₂ con probabilidad p y L₃ con probabilidad (1 – p), y esto para cualquier probabilidad p. Más formalmente, el axioma de independencia establece que, para cualquier L₁, L₂ y L₃, L₁ ≽ L₂ si y solo si [L₁, p, L₃, (1 – p)] ≽ [L₂, p, L₃, (1 – p)].

Clarifiquemos el axioma con un ejemplo:

	Ticket 1	Ticket 2-11
A	$1 M	$1 M
B	$0 M	$5 M

Tabla 1.

Te ofrecen la posibilidad de elegir entre las loterías A (que ofrece un premio seguro de $1 M) y B (que tiene una probabilidad de ganar $5 M de 10/11 o nada de 1/11). Si elegís A sobre B también deberías preferir ApB sobre ApC de la siguiente tabla.

	Ticket 1	Ticket 2-11	Ticket 12-100
ApC	$1 M	$1 M	$1 M
BpC	$0 M	$5 M	$1 M

Tabla 2.

vNM 4: (Continuidad) Si A ≻ B ≻ C entonces existe algún p y q tal que ApC ≻ B ≻ AqC

El siguiente ejemplo puede dar algo de claridad. Supongamos que A es un premio de $8 millones, B un premio de $7 millones y C un premio de $0. Según el axioma presentado, si preferís los $8 millones a los $7 millones y los $7 millones a $0, entonces debe existir alguna probabilidad p (no importa el número), tal que prefieras $8 millones con probabilidad p y $0 con probabilidad 1 − p en lugar de $7 millones con certeza. Asimismo, es necesario que exista alguna probabilidad q tal que prefieras $7 millones con certeza en lugar de $8 millones con probabilidad q y $0 con probabilidad 1 − q.

A partir de estos axiomas, se deriva un teorema llamado teorema de von Neumann-Morgenstern o teorema de la utilidad esperada (EU). El teorema establece que, si la relación de preferencia binaria ≽ del agente sobre las loterías satisface los axiomas enumerados anteriormente, entonces existe una función de valor real U(x) definida sobre el conjunto de resultados de las loterías, tal que, para cualquier par de loterías L₁ y L₂, el agente prefiere L₁ a L₂ si y solo si la esperanza matemática de la función U(x) calculada con respecto a L₁, es decir, ∑ L₁ U(x_i)p_i, es mayor que la esperanza matemática de U(x) calculada con respecto a L₂, es decir, ∑ L₂ U(x_i)p_i. En definitiva, L₁≽ L₂ si y solo si ∑ L₁ U(x_i)p_i ≥ ∑ L₂ U(x_i)p_i.

En este punto llegamos a la cuestión planteada al principio del capítulo. Los axiomas fueron el punto de partida para derivar a partir de ellos, un teorema. Las reglas lógicas de deducción (por ejemplo el principio de no contradicción) son la clave para poder demostrar cómo este teorema se deduce lógicamente de los axiomas. La prueba es larga y compleja^[4] pero la idea clave de los autores es demostrar que existe una función de utilidad u:X→R donde para todo x ∈ X se cumple que u(x) ∈ R asignando a cada alternativa x un número real que representa su utilidad, tal que la preferencia sobre loterías pueda representarse como la esperanza matemática de esta función. Para clarificar, X es el conjunto de elecciones y R los números reales. Así, de manera muy elemental la estrategia es suponer que existe un conjunto de premios posibles Z. Como el agente (por completitud) tiene preferencias ordenadas sobre Z, podemos identificar al mejor premio y al peor premio y por el axioma de continuidad se puede deducir cualquier otro premio A entre esos extremos con una probabilidad entre 0 y 1.

En resumen: a) los axiomas de completitud y transitividad garantizan una estructura ordenada de preferencias; b) el axioma de continuidad permite construir una función de utilidad creciente; c) el axioma de independencia impone una estructura lineal en la representación de preferencias; y d) se concluye que la función de utilidad es representable mediante la esperanza matemática.

Límites de la función de utilidad esperada: paradojas

Así como la noción de utilidad hace aparición precisamente por una paradoja (la de San Petersburgo) es otra paradoja la que le genera graves problemas y que inicia toda una serie de críticas que alcanzan hasta a la propia definición de racionalidad que subyace a la teoría (ser racional implica respetar los axiomas vNM).

La paradoja de Allais fue descubierta por Maurice Allais en 1952 y publicada al año siguiente, poco tiempo después de la aparición de la axiomatización propuesta por von Neumann y Morgenstern (Mongin, 2019, p. 2). Si bien puede entenderse como una crítica al teorema de la utilidad de manera integral, un análisis con cierta profundidad nos permitirá descubrir que es una crítica al axioma de independencia en particular.

Veamos el siguiente grupo de apuestas (adaptadas de Peterson, 2009, p. 79):

	Billete 1	Billete 2-11	Billete 12-100
Apuesta 1	$1 M	$1 M	$1 M
Apuesta 2	$0 M	$5 M	$1 M
Apuesta 3	$1 M	$1 M	$0 M
Apuesta 4	$0 M	$5 M	$0 M

Tabla 3.

En general, si una persona debe elegir entre la apuesta 1 o la 2, es razonable pensar que elegirá la 1, porque otorga de manera segura $1 millón. Asimismo, entre las opciones 3 y 4, en general, es razonable pensar que la persona elegirá 4, porque al haber alta probabilidad de no ganar nada, vale la pena el riesgo para obtener los $5 millones.

Ahora bien, calculemos la utilidad esperada de cada caso. De la apuesta 1 es u($1 M) x 1/100 + u($1 M) x 10/100 + u($1 M) x 89/100 = 1 y de la lotería número 2 es u($0 M) x 1/100 + u($5 M) x 10/100 + u($1 M) x 89/100 = 1.39. En este cálculo hemos tomado, en principio sólo el valor monetario, sin embargo, uno podría interpretar la utilidad de tal manera que sea preferible 1 a 1.39. Ahora bien si eso ocurre, en la elección entre la apuesta 3 y la apuesta 4, se debería cumplir el mismo criterio de definición de utilidad. Veamos el cálculo (apuesta 3): u($1 M) x 1/100 + u($1 M) x 10/100 + u($0 M) x 89/100 = 0.11. Y apuesta 4: u($0 M) x 1/100 + u($5 M) x 10/100 + u($0 M) x 89/100 = 0.5. En esta última elección, si el agente elige, tal como dijimos, la número 4 por sobre la 3, entonces entra en contradicción, porque el número de utilidad, si bien es mayor, no siguió ese mismo criterio en la elección anterior, puesto que 1 es menor a 1.39, y sin embargo, había optado por la opción de utilidad 1. De esta manera, la paradoja señala que las personas aplican inconsistentemente el principio de utilidad esperada.

Si miramos nuevamente las tablas 1 y 2, el axioma de independencia nos exige que si elegimos A sobre B, también deberemos elegir ApC sobre BpC. Y el ejemplo parecía razonable. Notemos, asimismo, que esas tablas representan las dos primeras líneas de la tabla 3. De esta manera, imaginemos una nueva variación en la tabla de modo tal que:

	Ticket 1	Ticket 2-11	Ticket 12-100
ApC	$1 M	$1 M	$0 M
BpC	$0 M	$5 M	$0 M

Tabla 4.

Nuevamente, si elegíamos A sobre B en la elección de la tabla 1 entonces debemos elegir, según el axioma de independencia, ApC sobre BpC, pero en este caso, parece razonable preferir BpC sobre ApC. El axioma de independencia exige que si la variación en las opciones es la misma, la elección se debe mantener, cuestión que no sucede en este ejemplo.

¿Qué es lo que muestra esta paradoja? Que es importante prestar atención al factor psicológico en la toma de decisiones. Pareciera que el agente se vuelve irracional cuando se presentan estos tipos de ejemplos, sin embargo, habría que pensar si los axiomas no necesitan cierta revisión o si existen mecanismos psicológicos necesarios a tener en cuenta cuando de decisiones se trata. Así, el mismo Allais señalaba que había que prestar atención al valor psicológico de los premios, por ejemplo, a la preferencia por la seguridad por parte de los agentes, es decir, que la seguridad es preferible ante cualquier desviación por mínima que sea (Parrondo, 2008, p. 77).

Y en este punto vislumbramos los límites de las posiciones normativas, por ejemplo, de la lógica. ¿Los axiomas y la teoría de la utilidad pretenden asimismo ser modelos descriptivos? No es una discusión que plantearemos aquí. Pero esta distinción entre normatividad y descripción es importante porque precisamente aquí es donde varios autores presentarán sus críticas a la teoría de la utilidad: los agentes no se comportan como la teoría plantea (v. Kahneman, 2020, p. 353). Uno puede considerar que Allais inició ese camino, sin embargo, se consideraba un heredero de Benoulli. No es sino hasta la segunda mitad del siglo XX cuando los experimentos en economía comenzaron a poner en cuestión los postulados de la racionalidad de los agentes (tal como estaban planteados en esas teorías).

De esta manera, pasemos brevemente a los estudios de Amos Tversky y Daniel Kahneman.

Teoría de las perspectivas

A. Piense en las siguientes loterías y luego tome una decisión (adaptadas de Kahneman, 2020, p. 365):

1. A su riqueza inicial se le añaden 1000 dólares. Elija entre las siguientes dos opciones: a) 50% de probabilidad de ganar 1000 dólares o b) 500 dólares seguros.

2. A su riqueza inicial se le han añadido 2000 dólares. Ahora, elija entre: a) 50% de probabilidades de perder 1000 dólares o b) perder 500 dólares con certeza.

B. Elija entre los siguientes pares de loterías (adaptado de Peterson, 2009):

1. c) $4 M; 0.8                         d) $3 M; 1

2. e) $4 M; 0.2                         f) $3 M; 0.25

C. ¿Aceptaría jugar el siguiente juego? (Adaptado de Kahneman, 2020, p. 369): Se lanza una moneda al aire, si sale ceca, pierde $100; si sale cara, gana $150.

   

La mayoría de las personas eligen el dinero seguro en el problema 1 del caso A. Sin embargo, en el segundo juego también del caso A, la mayoría prefirió jugar el juego. ¿Cuál es el problema de esto? Que para la teoría de la utilidad esperada no debería haber diferencias entre ambos casos porque implican la misma elección.

Si partimos desde la base de poseer 1000 dólares en el caso 1), el dinero seguro supone una ganancia de 500 dólares, mientras que en el problema 2), al partir de la base de 2000 dólares, finalizar el juego con 1500 supone una pérdida. Lo mismo sucede con el caso C, evidentemente el valor esperado del juego es positivo (Kahneman, 2020, p. 369) pero la mayoría de la gente no querrá jugarlo.

Por último, en el caso B, encontramos la violación del principio de independencia. Este ejemplo es una reformulación de la paradoja de Allais. Entre c) y d) la mayoría de las personas optaron por el dinero seguro, mientras que entre e) y f), se prefirió la primera de las opciones. El problema es que 2) puede entenderse como ¼ de probabilidad de los casos de 1) por lo que si se prefería d) sobre c) debería también preferirse f) sobre e).

¿Qué es lo que sucede con estos casos? La propuesta de Kahneman y Tversky es que es necesario sumergirse en el campo de la psicología experimental descriptiva para poder entender la propuesta normativa económica y reformularla, para que pueda responder a las acciones de los seres humanos de carne y hueso. Como habíamos señalado al inicio de este capítulo, la lógica y el concepto de racionalidad clásico encuentran su límite cuando los seres humanos no responden a cómo esos modelos ideales esperan que actúen.

Dicho esto, la corriente de las heurísticas y los sesgos de Kahneman y Tversky no llama a abandonar el barco de los modelos normativos sino revisar la faceta psicológica de la toma de decisiones. En este sentido, no pretenden desechar la función de la utilidad esperada, sino reformularla, teniendo en cuenta los condicionantes psicológicos de los seres humanos. Y así, estos autores intentarán resolver problemas como la paradoja de Allais, pero, más importante aún, buscarán dar mayor poder predictivo a estas fórmulas de decisiones bajo riesgo.

El primer elemento que hay que tener en cuenta en esta revisión de la teoría económica clásica es la noción de “punto de referencia” (Kahneman, 2020, p. 366). Recordemos que Bernoulli había pensado en el patrimonio inicial a la hora de evaluar la utilidad de un premio, sin embargo, carecía de una parte emotiva. Teniendo esto en cuenta, ese estado de referencia hace alusión a la situación anterior desde la cual se van a evaluar las ganancias y las pérdidas (Kahneman, 2020, p. 366). Precisamente, en los ejemplos citados más arriba, particularmente en el A, el punto de referencia indicaba si esa elección implicaba una ganancia o una pérdida.

El segundo principio que hay que tener en cuenta (que nos recuerda a la revisión de Bernoulli a la noción de valor esperado) es que la diferencia subjetiva entre montos de más altos es menor que a las diferencias entre montos más bajos.

Por último, la “aversión a las pérdidas” (Kahneman, 2020, 369) es un principio psicológico que describe que para los seres humanos las pérdidas pesan más que las ganancias, y por eso, en el ejemplo C la mayoría de las personas no quieren jugar al juego.

La siguiente gráfica muestra los tres principios representados (adaptada de Kahneman, 2020, p. 368):

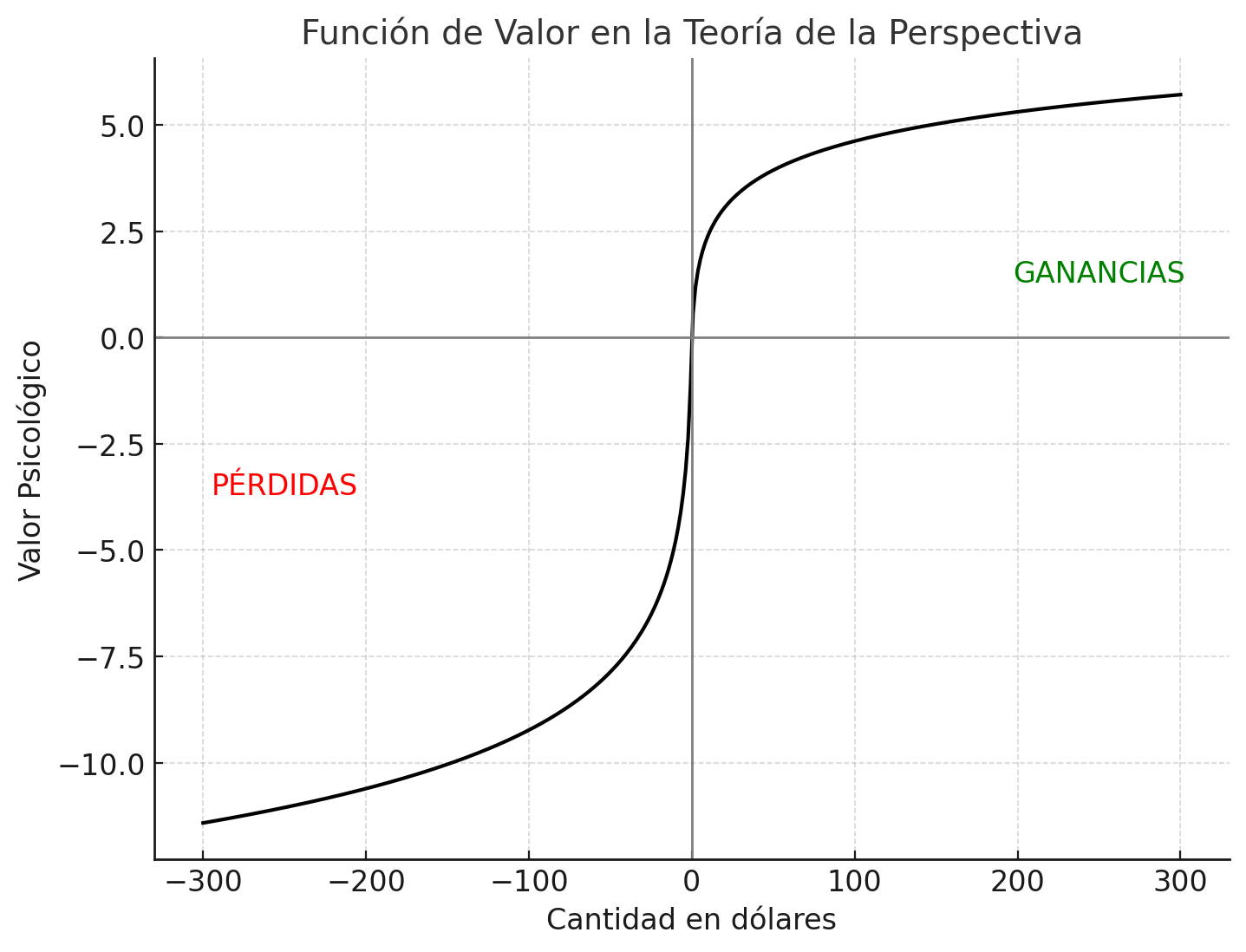
Figura 2. Función hipotética de ponderación de valoración.

La gráfica en forma de S nos muestra la disminución de la sensibilidad a las ganancias, así también como a las pérdidas y fundamentalmente, el cambio desde el punto de referencia neutral: las pérdidas generan una respuesta más abrupta que las ganancias.

Existen otros elementos además de los tres mencionados que el enfoque de las heurísticas y los sesgos fueron descubriendo a través de la experimentación, sin embargo, no podríamos tratarlos todos aquí. Uno que sí vale la pena mencionar es que las personas interpretan a las probabilidades, muchas veces, de manera errónea, dependiendo de cómo se presenten y de qué tan pequeñas sean. Así, por ejemplo, si se les pedía a las personas que eligieran entre A o B y C o D:

A: ($6,000, 0.45)

B: ($3,000, 0.9)

C: ($6,000, 0.001)

D: ($3,000, 0.002)

elegían B por sobre A pero C por sobre D. Si entendemos que la lotería C y la D son una reformulación de A y B respectivamente (puesto que se les multiplicó por 1/450 de probabilidad), notaremos que sucede una violación del axioma de independencia. La cuestión novedosa aquí radica en la imposibilidad de interpretar correctamente probabilidades tan pequeñas (Peterson, 2009, 287).

Teniendo en cuenta todos los elementos anteriores descubiertos por la escuela de las heurísticas y los sesgos, Kahneman y Tversky formulan la teoría de las perspectivas. La función de utilidad esperada que ponderaba la probabilidad por la utilidad se revisa teniendo en cuenta dos funciones nuevas de ponderación (Peterson, 2009, p.289).

w (p₁) . v (u₁) + w (p₂) . v (u₂) + … + w (p_n) . v (u_n)

Así, w se asocia a las probabilidades porque da cuenta de que las personas sobreestiman las pequeñas probabilidades pero subestiman las grandes. Es la experimentación la que determinará el valor de w, es decir, es una cuestión empírica. Por otra parte, v queda representada por la función de la figura 2 , es decir, representa el peso de las pérdidas y las ganancias a partir de un cierto punto de referencia.

Conclusión

Hemos realizado un repaso sobre el concepto de utilidad pero teniendo en cuenta que nuestro propósito era mostrar el valor y los límites de la lógica. La teoría de la utilidad esperada desde la versión de von Neumann y Morgenstern es una muestra de la importancia de las reglas de inferencia en un sistema axiomático. Los autores lograron justificar lo que Bernoulli sólo pudo presentar. Las posiciones axiomáticas muestran ser más sólidas frente a los argumentos presentados sobre la ley de los grandes números.

Sin embargo, los modelos normativos también tienen sus límites, y eso quedó claro cuando se sumaron a la discusión elementos de psicología experimental. Los seres humanos no son “econs” (Sunstein, C.; Thaler, R., 2017, p. 16) en el sentido de sujetos egoístas y racionales que ponderan costos y beneficios. Sino que existen otros elementos para tener en cuenta, como nos ha demostrado la teoría de las perspectivas. Si queremos predecir con mayor exactitud el comportamiento humano será necesario estudiar cómo las personas toman decisiones y razonan en contextos reales, cuestión adeudada principalmente por los modelos racionalistas. Aunque también, es justo decir, por muchos modelos descriptivos que marcaron un nuevo camino pero que muchas veces siguen manteniendo a esos modelos como ideal. No entraremos en eso aquí pero un buen punto de partida puede ser incursionar en las teorías de la escuela de las heurísticas rápidas y frugales (Gigerenzer, 2008) para revisar el propio concepto de racionalidad y para intentar resolver la dicotomía planteada en la cita inicial: la psicología puede mostrarnos qué significa ser racional más allá de los modelos ideales.

Bibliografía

Gigerenzer, G. (2008). Rationality for mortals. Oxford University Press.

Gigerenzer, G. (2002). Adaptative thinking. Nueva York, Oxford University Press.

Gilboa, I. (2011). Making better decisions. Singapore, Wiley-Blackwell.

Hintikka, J. (2009). “What is the axiomatic method?” en Synthese (2011) 183:69–85. Springer.

Hintikka, J.; Sandu, G. (2007). “¿Qué es la lógica?” en Frápolli Sanz, M. (2008). Filosofía de la lógica. Tecnos.

Kahneman, D. (2020). Pensar rápido, pensar despacio. Buenos Aires, Debate.

Keynes, J. (1992). Breve tratado sobre la reforma monetaria. México D.F., FCE.

Mongin, P. (2019). “The Allais paradox: what it became, what it really was, what it now suggests to us” en Economics and Philosophy. Cambridge University Press.

Moscati, I. (2023). The history and methodology of expected utility. Cambridge University Press.

Parrondo, J. (2008). “Sortis in ludis: de la paradoja de San Petersburgo a la teoría de la utilidad” en Conferències FME Volum 4. Barcelona, Barcelona Digital.

Peterson, M. (2009). An introduction to decision theory. Cambridge, Cambridge University Press.

Resnik, M. (1998). Elecciones. Barcelona, Gedisa.

von Neumann, J.; Morgensten, O. (1953). Theory of games and economic behavior. Princeton, Princeton University Press.

Sunstein, C.; Thaler, R. (2017). Un pequeño empujón. Barcelona, Penguin.

---