Josefina Schneeberger

Existen relaciones íntimas, profundas, esenciales entre el psicoanálisis y la lógica.

    

Jacques Lacan, Seminario 12

Introducción

Jacques Lacan (1901-1981) psiquiatra y psicoanalista francés, es conocido por sus novedosos aportes a la teoría psicoanalítica a partir de la relectura de Freud por medio de herramientas conceptuales tomadas de otras disciplinas como la lingüística, la filosofía, el arte, las matemáticas y la lógica. En este capítulo nos centraremos en los conceptos que el psicoanalista francés toma de esta última.

De esta manera, el objetivo será analizar el uso que Lacan hace de la lógica, especialmente teniendo en cuenta que cuando toma conceptos de otras disciplinas, los altera para aplicarlos al psicoanálisis y, además, en ese proceso, altera de raíz al psicoanálisis también.

Si bien Lacan ha demostrado interés por la lógica a lo largo de toda su obra y podemos identificar referencias a esta disciplina en distintos momentos de su enseñanza, nos centraremos en una de sus últimas conceptualizaciones, las fórmulas de la sexuación, considerando que es en este punto donde Lacan establece los diálogos más cercanos con la lógica. Éstas tienen como objetivo dar cuenta del arribo a cierta posición sexuada por vía de la lógica y no de la diferencia anatómica de los sexos, estableciendo la imposibilidad de la relación sexual. En este capítulo nos limitamos a explicitar las herramientas que Lacan toma de la lógica y de qué manera las utiliza, y no abordaremos las consecuencias clínicas de las fórmulas de la sexuación.

Lacan empieza a elaborar sus fórmulas de la sexuación en su Seminario 18, De un discurso que no fuera del semblante en el año 1971 y continúa en El Seminario 19, … O peor. Finalmente, en el año 1973 presenta la versión definitiva de las fórmulas en El Seminario 20, Aún (Encore). Es así como, a partir de la lectura y análisis de estos tres seminarios, iremos develando las distintas herramientas teóricas que Lacan toma de la lógica para escribir las fórmulas de la sexuación. Trazamos un recorrido lógico por las lecturas que hace Lacan de los lógicos Peirce, Frege y Russell, y de las que se servirá para formular el “no-todo”. Aquí la novedad lacaniana, al negar el cuantificador mismo, distanciándose de Aristóteles. Para el filósofo griego, la negación de un universal tiene como consecuencia un universal de signo contrario. En cambio, Lacan al poner la barra de la negación sobre el cuantificador, abre la posibilidad de abordar, a través del no todo, la imposibilidad de escribir la relación sexual.

Jacques Lacan, algunas aclaraciones sobre su obra

Cuando nos referimos a la obra de Lacan resulta necesario hacer algunas aclaraciones, ya que más allá de su tesis de doctorado De la psicosis paranoica en sus relaciones con la personalidad (1932), Lacan no firmó como propio ningún libro. En lugar de eso nos encontramos con dos tipos de materiales: los Escritos y El Seminario. Los primeros son un compilado de artículos publicados en distintas revistas, mientras que El Seminario constituye la vertiente oral y es considerado el lugar donde se elabora el pensamiento lacaniano. Comienza en 1953 y duró hasta 1980. Fueron casi treinta años de enseñanza, desarrollados en 27 tomos, que actualmente no fueron publicados todos, salvo en ediciones no oficiales. En un inicio Lacan se negó a la publicación de sus seminarios, hasta que en el año 1973 aceptó que Jacques-Alain Miller estableciera el texto sobre la base de grabaciones y transcripciones, lo que resultó en la coautoría legal.

La consigna que organizó el proyecto lacaniano fue el “retorno a Freud”. Esto supone releer a Freud, dando cuenta del descubrimiento freudiano del inconsciente, formalizando y teorizando acerca de este descubrimiento. Lacan no intenta hacer entrar a la teoría freudiana en el molde ya existente de la nosografía psiquiátrica, sino que, por el contrario, invierte el orden de las cosas para introducir la primacía del inconsciente en el estudio clínico (Roudinesco, 1993, p. 123). Por lo tanto, para Lacan fue necesario reanudar la lectura de los textos de Freud para delimitar los fundamentos de una práctica, que con los post-freudianos fue virando hacia una técnica contraria a los principios mismos del psicoanálisis.

El interés de Lacan en la lógica

Resulta conocido que Lacan mantuvo un diálogo constante, aunque no siempre explícito, con las disciplinas de su tiempo tales como la filosofía, la lingüística, el arte y la lógica. El interés de Jacques Lacan por esta última es constante a lo largo de toda su obra, no hay uno solo de los 27 Seminarios que impartió entre 1953 y 1980 que no haga referencia a la lógica de manera más o menos amplia (Gutiérrez Arconada, 2023, p. 12). Lacan ha señalado en numerosas ocasiones la necesidad de que el analista se familiarice con la disciplina lógica-matemática, a tal punto que sostiene que la propia práctica analítica conduce inevitablemente al estudio de la lógica (Gutiérrez Arconada, 2023, p. 14)

No en vano los conmino a no omitir nada de lo que se produce en el orden de la lógica. […] Sin una referencia lógica a la lógica clásica, aristotélica, que, por supuesto no puede bastar, es imposible hallar el punto justo en los temas que presento. (Lacan, 2009, pp. 124 y 158)

El interés de Lacan en la disciplina lógica se debe en parte al intento de formalizar el psicoanálisis, es decir, de encontrar un medio que lo haga universalmente transmisible, condición de la ciencia moderna. Para tal fin, recurre a las matemáticas, la topología y la lógica. A lo largo de su obra, emprenderá esta tarea de formalización por medio de los esquemas, los grafos, los matemas, la topología y las fórmulas de la sexuación.

Lacan consideraba que es imprescindible que los psicoanalistas tengan algún conocimiento sobre lógica. Por eso, cuando en 1975 formula el programa de enseñanzas de la formación universitaria del departamento de Psicoanálisis en la Universidad de París VIII en Vincennes, incluye a la lógica “a condición de que sea destacada como ciencia de lo real por permitir el acceso a ella del modo de lo imposible” (Lacan, 2007, p. 334). Ya con esta definición de la lógica, podemos notar que la manera de entender las herramientas lógicas difiere del sentido que se les dio en su campo de origen.

¿A qué llama lógica Lacan?

La lógica es concebida por Lacan como una herramienta necesaria en la búsqueda de lo real, de ahí que la defina como ciencia de lo real. Ahora bien, no debemos confundir lo real con la realidad. Lo real es un término tan opaco como aquello que viene a delimitar. Lacan teoriza que la realidad humana se compone de tres registros: simbólico, imaginario y real. El registro de lo real es no asimilable por la palabra, es no representable, es lo no posible de apresar por el significante. Dos dimensiones en las que aparece lo real son la muerte y la sexualidad, porque no hay representación posible: no lo podemos pensar, imaginar, representar, conceptualizar. Así como no podemos representar nuestra propia muerte, Lacan dirá que ocurre lo mismo en lo que atañe a la relación sexual.

Lacan buscará formalizar lo real por medio de la letra, de la escritura, como orden distinto al de la palabra. Es en el Seminario 18, De un discurso que no fuera del semblante, donde Lacan empieza a marcar la diferencia entre el significante y la letra, más precisamente entre lo que es del orden de la palabra y lo que es del orden de lo escrito. Y dirá que la lógica remite a este último. Se trata de escritura en el sentido amplio: Lacan estará pensando en los esquemas, los grafos y las fórmulas como formas de escritura.

La lógica se abre como ciencia de lo real a partir de la posibilidad de vaciar bastante de su sentido a las palabras para sustituirlas por letras. Lacan sostiene: “Consiste en hacer agujeros en lo escrito. Todos los animales son mortales, quitan animales y quitan mortales, y ponen en su lugar el colmo de lo escrito, es decir, una simple letra” (Lacan, 2009, pp. 73-75). La lógica permite reemplazar los términos de las proposiciones por letras y de esta manera despojarlos del sentido que los términos implican, y este es el camino en el acceso a lo real. Con “hacer agujeros en lo escrito” Lacan refiere al intento de bordear o aproximarse a lo que está más allá de lo que puede decirse o escribirse, es decir, a lo real, marcando los límites del lenguaje y de lo simbólico. De esta manera, Lacan piensa lo escrito como borde de lo real. La escritura nos permite acercarnos a lo real, pero en sí mismo lo real es ese imposible que no puede escribirse. Lo que no se escribe tiene que ver con la relación sexual. Esto es lo que Lacan busca representar por medio de su célebre frase “la relación sexual no existe”, que encontrará su plena extensión lógica por medio de la construcción de las fórmulas de la sexuación, que vemos a continuación (Le Gaufey, 2007, p. 8).

Las fórmulas de la sexuación, una construcción lógica

Lacan empieza a escribir sus fórmulas de la sexuación en su seminario De un discurso que no fuera del semblante en el año 1971 y continua a lo largo de El Seminario 19, … O peor y El Seminario 20, Aún (Encore). Iremos haciendo un recorrido por los tres seminarios, siguiendo los pasos lógicos de Lacan, para culminar en la versión final de las fórmulas de la sexuación escritas en el capítulo VII del Seminario 20, Aún, que presentamos a continuación.

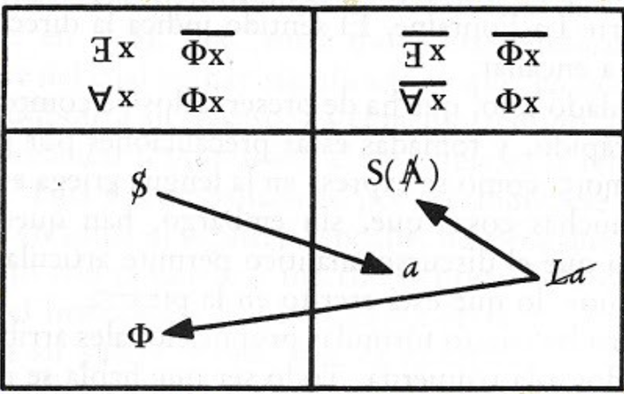
Fórmulas de la sexuación presentadas en el capítulo VII, “Una carta de amor”, de El Seminario XX, Aún.

Nos limitaremos a abordar la parte superior del cuadro donde se observan las cuatro fórmulas propuestas por Lacan. Las fórmulas se escriben con una función F(x), con las negaciones (la barra encima de una función o un cuantificador) y con los operadores lógicos llamados cuantificadores, que corresponden al signo “para todo” y al signo “existe al menos uno”.

Si Freud pensaba que la anatomía es el destino, Lacan separa lo masculino y femenino de lo fisiológico para plantearlo como dos lógicas diferentes: la lógica del todo y la excepción del lado masculino (lado izquierdo de las fórmulas) y la del no todo del lado femenino (lado derecho de las fórmulas). Todo ser que habla se inscribe en uno u otro lado de las fórmulas.

Las fórmulas de la columna de la izquierda inscriben al sujeto en la posición masculina y deben leerse del siguiente modo: “Existe un x que no phi de x” y “Para todo x phi de x”. Las de la columna de la derecha e inscriben al sujeto en la posición femenina y se leen de la siguiente manera: “No existe un x que no phi de x” y “No todo x, phi de x”.

Iremos desglosando las fórmulas analizando cada uno de sus elementos y las referencias lógicas utilizadas. Comenzamos por Charles Sanders Peirce, y su particular lectura de las proposiciones aristotélicas, siguiendo por el uso de los cuantificadores lógicos y su posible negación, que dará lugar al invento lacaniano del “no-todo”. Nos remitimos al concepto de función del lógico alemán Gottlob Frege, y a Bertrand Russell y su conocida paradoja lógica, que Lacan retoma para escribir las fórmulas.

Del mito a la lógica. Una lectura de Tótem y tabú desde la propuesta de Charles Sanders Peirce

En el Seminario 18, De un discurso que no fuera del semblante, Lacan distingue aquello que es del orden del significante de lo que es del orden de lo escrito, y a partir de esto lee el mito freudiano Tótem y Tabú desde la lógica.

¿Qué quiere decir el mantenimiento en el discurso analítico de este mito residual llamado el mito del Edipo, sabe Dios por qué, que es de hecho el de Tótem y tabú, donde se inscribe el mito, enteramente inventado por Freud, del padre primordial por cuanto goza de todas las mujeres? Debemos interrogar esto un poco más allá, desde la lógica, desde lo escrito. Hace mucho tiempo introduje aquí el esquema de Peirce relativo a las proposiciones… (Lacan, 2009, pp. 63-64)

La frase “todas las mujeres” tendrá una importancia crucial en la medida en que Lacan pretende negarla, sostener que no existe el conjunto de todas las mujeres. Comienza un cuestionamiento al sostenimiento de la universal y afirmará que “todas las mujeres” no existe, valiéndose de la propuesta de Peirce.

Empecemos recordando el mito freudiano de Tótem y tabú. Se trata de una historia mítica por medio de la cual Freud pretendía resolver problemas de psicología individual recurriendo al material de la psicología de los pueblos. En Tótem y tabú. Algunas concordancias en la vida anímica de los salvajes y de los neuróticos (1913 [1312-1913]) Freud relata que en la horda primordial existía un padre violento, celoso, que se reservaba todas las hembras para sí y expulsaba a los hijos varones cuando crecían. Un día los hermanos expulsados se aliaron, mataron y devoraron al padre. Sin embargo, luego del asesinato del padre se produjo una obediencia de efecto retardado (nachträglich). Revocaron su hazaña declarando no permitida la muerte del sustituto paterno, el tótem, y establecieron la prohibición del incesto, instaurando de esta manera, la ley igual para todos (Freud, 1913, pp. 143-146)

Para pasar del mito a la lógica, Lacan introduce el esquema del filósofo Charles Sanders Peirce.^[1]

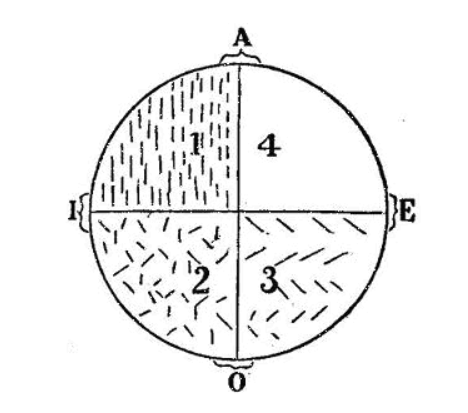
Esquema de Peirce (2003).

El lógico estadounidense retoma las cuatro formas proposicionales propuestas por Aristóteles: Universales Afirmativa (A), Universal Negativa (E), Particular Afirmativa (I), Particular Negativa (O). Sin embargo, lo hará para cuestionar la posición de Aristóteles, quien supone que la proposición Universal Afirmativa implica la existencia del sujeto. Peirce (2003, s/p) declarara que “las proposiciones universales no implican la existencia de sus sujetos, mientras que las particulares sí”. Este punto es justamente el que despierta el interés de Lacan:

Si el esquema de Peirce, Charles Sanders, tiene un interés, es mostrar que definir que todo x es y, que toda cosa está provista de tal atributo, es una formulación universal perfectamente admisible sin que haya sin embargo ningún x. (Lacan, 2009, p. 64)

Por medio del esquema presentado busca ilustrar el sentido preciso de las proposiciones A, E, I, O. En el cuadrante marcado con el número 1 hay líneas que son todas verticales; en el cuadrante marcado con el 2 algunas líneas son verticales y algunas no; en el cuadrante 3 ninguna de las líneas es vertical; y en el cuadrante 4 no hay líneas. Ahora bien, tomando línea como sujeto y vertical como predicado tendríamos:

A (Toda línea es vertical) es verdadero de los cuadrantes 1 y 4 y falso del 2 y 3.

E (Ninguna línea es vertical) es verdadero de los cuadrantes 3 y 4 y falso del 1 y 2.
I (Alguna línea es vertical) es verdadero de los cuadrantes 1 y 2 y falso del 3 y 4

O (Alguna línea no es vertical) es verdadero de los cuadrantes 2 y 3, falso del 1 y 4.

A partir de esto, Peirce retoma el diagrama de Apuleyo o cuadro de oposición de juicios, para diferenciarse de Aristóteles.

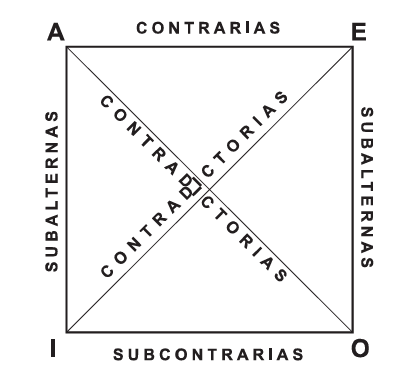
Cuadro de oposición de juicios.

Critica la designación que hace Aristóteles de contrarias entre Universales Afirmativas y Universales Negativas, ya que para Aristóteles podrían ser ambas falsas, pero no ambas verdaderas. Si para Aristóteles la afirmación “Toda línea es vertical” es contraria a “Ninguna línea es vertical”, en la medida en que ambas no pueden ser verdaderas juntas, Peirce propone con su sistema una subversión al tomar juntos al cuadrante 1 y 4 (Iuale, 2017, p. 107). Y afirma que A y E son verdaderas juntas cuando no existe ninguna línea, y son falsas juntas cuando solo parte de las líneas son verticales. De esta manera, da cuenta de que las proposiciones universales no suponen existencia. Puede que no exista ninguna línea, haciendo que tanto la Universal Afirmativa como la Universal Negativa sean verdaderas.

Con respecto a las proposiciones I y O, que Aristóteles designa como subcontrarias, donde podrían ser ambas verdaderas, pero no ambas falsas, Peirce en cambio propone que ambas son verdaderas o ambas falsas en condiciones opuestas. Es decir, que son verdaderas ambas cuando solo parte de las líneas son verticales y falsas cuando no existe ninguna línea vertical. Este punto influenciará a Lacan para entender la proposición particular en su sentido máximo y no en el sentido mínimo que Aristóteles privilegió (Le Gaufey, 2007, p. 103). Si tenemos “algunos S son P”, el sentido mínimo es “todos los S pertenecen a P”. De esta manera, las proposiciones particular y universal son verdaderas. Podríamos decir que el particular se deduce de la universal. Si seguimos el sentido máximo de la particular, debemos entender “algunos S son P” como “no todos los S son P”. Esta lectura va a incidir en Lacan, especialmente en la formulación del “no-todo”, elemento imprescindible en la construcción de las fórmulas de la sexuación.

Peirce (2003) también modificará las relaciones entre A e I, que serán verdaderas juntas cuando toda línea es vertical y son falsas juntas cuando haya líneas de las cuales ninguna es vertical, y entre E y O, que serán verdaderas y falsas juntas precisamente bajo las circunstancias opuestas.

Por ende, en el sistema de Peirce (2003, s/p) “no se preserva ninguna de las relaciones mostradas en el diagrama de Apuleyo (el cuadrado de oposición), excepto los dos pares de contradictorias. Todos los otros pares de proposiciones pueden ser verdaderas juntas o falsas juntas”

A partir de estos desarrollos, Lacan interpela el mito de Tótem y Tabú. Como ya hemos adelantado, una primera consecuencia que el psicoanalista extrae es que “lo que muestra el mito del goce de todas las mujeres es que no hay todas las mujeres. No hay universal de la mujer.” (Lacan,2009, p. 64). Es el mito de Tótem y tabú el que apunta a que no hay todas las mujeres, que Lacan equipara, valiéndose del esquema de Peirce, al hecho de que poder decir “Todo S es P” como universal es perfectamente compatible con el hecho de que no haya ningún S.

el mito escrito, Tótem y tabú, está hecho exactamente para indicamos que es impensable decir La mujer. ¿Por qué es impensable? Porque no puede decirse todas las mujeres. No puede decirse todas las mujeres porque esto solo se introduce en este mito en nombre de que el padre posee a todas las mujeres, lo que es manifiestamente el signo de una imposibilidad. (Lacan,2009, pp. 98-99)

El padre que goza de todas las mujeres es el mito que permite que lo real se encarne, respecto del goce sexual, como imposible (Iuale, 2017, p. 109). El padre de la horda primordial es anterior a la instauración de la ley igual para todos, de manera que puede poseer a todas las mujeres. En este sentido, no está castrado, se trata de un padre mítico en tanto que no está sometido a la función fálica (la castración), que Lacan representará por medio de la letra griega Φ. Por lo tanto, La mujer, en calidad de todas las mujeres, no existe más que en este momento mítico. De ahí que Lacan dirá que “La mujer no existe”, comenzando los primeros esbozos de la lógica del no-todo para pensar lo femenino.

El Padre es un mito, porque salta a la vista en efecto que Φx no anda en el nivel de Tótem y tabú. El Padre no está castrado; en caso contrario, ¿cómo podría tener a todas? ¿Se dan cuenta? Además, ellas existen en calidad de todas solamente allí, ya que a las mujeres conviene el no-todo. (Lacan, 2012, p. 36)

Los cuantificadores y las primeras escrituras

Para avanzar en la construcción de las fórmulas de la sexuación, Lacan se propone pasar de la lógica aristotélica a las proposiciones de la lógica matemática por medio de los cuantificadores (Lacan, 2009, p. 102), a los que llamará cuantores: “Por lo general se los denomina cuantificadores, pero prefiero llamarlos cuantores –no soy el único ni el primero– porque lo importante es que ustedes sepan que nada tienen que ver con la cantidad, lo que es evidente” (Lacan, 2012, pp. 34-35).

En la clase del 17 de marzo de 1971, Lacan se va a valer de los cuantificadores para representar las cuatro proposiciones aristotélicas.

Lacan (2009): El Seminario 18, p. 102.

Si nos detenemos en la Universal Negativa ∀x.F(x) y en la Particular Negativa ∃x.Fx, podemos observar una manera no clásica de usar la negación haciéndola que se refiera no al conjunto de la proposición, sino a cada uno de sus componentes (Le Gaufey, 2007, p. 85). Con la negación de la universal, Lacan dice inventar lo que denomina “el no-valor de la universal negativa”. En este momento de su enseñanza, ya tiene en mente su “no existen todas las mujeres”, que intentará ubicar en ese sitio. A partir de esto, sostiene:

(…) quedó de algún modo descuidada, sin valor, la universal negativa, en la medida en que permite decir que no debe escribirse F(x) de cualquier x que se hable. En otras palabras, aquí funciona un corte esencial. Pues bien, en torno de esto mismo se articula lo que atañe a la relación sexual. (Lacan, 2009, p. 103)

Un mes después, en la clase del 19 de mayo de 1971, considera absurda su primera escritura de la universal negativa y se produce el desplazamiento: la barra negativa ya no debe recaer sobre la función sino sobre el cuantificador ∀x Φx. Ahí aparece el invento y la posibilidad de abordar, a través del “no-todo” (∀x), lo imposible de escribir: la relación sexual.

Tal vez hayan notado que ni siquiera se me ocurrió, por lo menos hasta ahora, tampoco a ustedes, que la barra de la negación tenía tal vez algo que hacer, que decir, en la columna, no de la derecha, sino de la izquierda. Veámoslo. ¿Qué provecho podemos sacar de esto? (Lacan, 2009, p. 130)

A partir de este momento la función F(x) será la función fálica y la sexuación se ordenará en torno a dicha función (Iuale, 2017, p. 111). La función fálica tiene el valor de la castración y Lacan la escribe con la letra phi mayúscula Φ.

El concepto de función en Frege

Lacan toma el concepto de función de Gottlob Frege para construir las fórmulas de la sexuación. Frege (1998, p. 59) postula que “(…) la expresión de una función tiene que mostrar siempre uno o más lugares que están destinados a ser llenados por el signo del argumento”. Generalmente, éste se escribe con la letra x. De modo que para escribir una función “uno se sirve, en la mayoría de los casos, de las letras f y F de modo que en f(x) y F(x), x está por el argumento” (Frege, 1998, p. 62). Tal signo sólo hace referencia a un lugar, pero no a los posibles objetos que pueden ocuparlo de manera que no se debe considerar a la “x” de una función como parte ontológica de la misma. En otras palabras, se trata solamente de un vacío destinado a ser ocupado por un argumento que no forma parte de la función. Teniendo en cuenta esta esencia de la función se explica que, por un lado, reconozcamos en «2 · 1³ + 1» y «2 · 2³ + 2» la misma función, aunque estas expresiones se refieran a números distintos, mientras que, por otro lado, no encontramos la misma función en «2 · 1³ + 1» y «4-1» a pesar de su mismo valor numérico.

La importancia del concepto de función en Frege trasladado a las fórmulas de la sexuación radica en que, en primer lugar, al no tratar al argumento como parte ontológica de la función, si bien decimos “para todo x phi de x” podría darse el caso que ningún x viniera a ocupar el lugar vacío y la función seguiría siendo válida (Guilañá, 2017, p. 5). En segundo lugar, y por la misma razón que en el caso anterior, esta “x” ocupa un lugar vacío que cualquier argumento puede venir a ocupar. En las fórmulas de la sexuación, la x no define a la función a partir de ciertas características que se le podrían atribuir a x. Por ejemplo, no se trata de pensar a “x” como cuerpo biológico masculino o femenino, sino que cualquier “x” que cumpla con la función F(x) y que, en consecuencia, tenga todo su goce sexual ordenado por tal función, entonces, diremos que “x” está en posición masculina en relación a su goce. Paralelamente, diremos que, si no todo el goce de “x” está ordenado por la función fálica, entonces, “x” está en posición femenina.

Lógica de conjuntos y la paradoja de Russell

Continuamos nuestro recorrido lógico. Ya hemos visto las referencias de Lacan a Charles Sanders Peirce y su lectura de las proposiciones aristotélicas, siguiendo por el uso de los cuantificadores lógicos y el concepto de función de Frege. Ahora nos referimos a Bertrand Russell y su conocida paradoja lógica, que Lacan toma para terminar de escribir las fórmulas de la sexuación en el seminario XX.

Siguiendo la lógica aristotélica, el enunciado particular o existencial se deduce del universal (“Si todos los hombres son mortales, y Sócrates es un hombre, entonces, Sócrates es mortal”). Para Aristóteles, entre la Universal Afirmativa y la Particular Afirmativa, y entre la Universal Negativa y la Particular Negativa, hay una relación lógica de implicación. Sin embargo, para Lacan existe también una cierta implicación entre el universal y el particular, pero de una manera muy distinta puesto que el existencial es aquello que posibilita un decir universal, es su condición de posibilidad misma. En consecuencia, se invierte la posición aristotélica siendo el particular el que posibilita el universal y no viceversa. Aquí la referencia es Russell y la paradoja lógica que encontró en los Fundamentos de la Aritmética de Frege. En 1902 Russell le envía una carta a Frege enunciando la paradoja que inicio la crisis de los fundamentos en matemáticas. Para explicar esta paradoja partimos de la base de que los conjuntos pueden ser de dos tipos: los que se contienen a sí mismos y los que no. Un ejemplo de los primeros sería el conjunto de las cosas pensables que en sí mismo es una cosa pensable y el otro, el conjunto de los filósofos que en sí mismo queda claro que no es un filósofo y, en consecuencia, no se contiene a sí mismo. Si consideramos un conjunto como el conjunto de los conjuntos que no se contienen a sí mismos entramos en una doble contradicción. Por un lado, si el conjunto que engloba a todos los conjuntos que no se contienen a sí mismos se contiene a sí mismo es una paradoja. Pero si no se contiene a sí mismo su misma definición implica que se contiene a sí mismo de manera que volvemos a caer en otra contradicción.

Por lo tanto, lo que demuestra la paradoja de Russell es que para que pueda haber un conjunto cerrado debe haber un límite externo que lo cierre. Un conjunto se traza delimitando lo que pertenece y lo que no pertenece a él, lo que queda fuera. Esto se puede leer en términos de excepción, es lo que comúnmente se dice con la expresión “la excepción confirma la regla”. Y esto es lo que Lacan usará para leer Tótem y tabú. La excepción, el padre que gozaría de todas las mujeres, es lo que permite cerrar el conjunto de los iguales sometidos a la ley de la castración. Es lo que Lacan va a llamar la función del al-menos-uno.

Por eso es indispensable el al menos uno en que se sostiene el Nombre-del-Padre mítico. Al decirlo planteo la apreciación que falta a la noción de especie o de clase, y que muestra bien que no por casualidad en las formas aristotélicas toda la dialéctica fue fallida. ¿Dónde funciona en fin ese, ese existe al menos uno que no es siervo de la función fálica? (…) Pero observen que, con respecto a la universal señala da como, todo macho es siervo de la función fálica. ¿Qué quiere decir este al menos uno que funciona por escapar a ella? Diré que es la excepción. Es lo que dice, sin saber lo que dice, el proverbio La excepción confirma la regla. Es singular que solo con el discurso analítico un universal pueda encontrar su fundamento verdadero en la existencia de la excepción. El universal así fundado en todo caso se distingue de todo uso del susodicho universal que la tradición filosófica haya vuelto común. (Lacan, 2012, p. 105)

En el mito freudiano es el asesinato del padre lo que borra la excepción del que gozaría de todas las mujeres y con eso instaura la ley igual para todos. En la lectura que hace Lacan, el mito freudiano describe la función del “no-más-de-uno” como origen de lo universal. Se trata de un hecho de estructura, es necesario ese lugar de excepción del padre de la horda, para que se pueda decir de todo hombre que está sujeto a la castración. Se trata de un goce permitido para todos los hombres, pero este será un goce limitado, castrado, lo que va a designar con la función Φx.

Paralelamente ya no puede decirse todas las mujeres, porque en el lado femenino no hay un lugar de excepción que funde el conjunto de todas las mujeres como conjunto cerrado. El conjunto de todas las mujeres solo existe en el momento mítico en el que el padre goza de todas. De esta manera, a la posición femenina le corresponde el no-todo, que Lacan se esfuerza en construir.

La versión final de las fórmulas de la sexuación

Fórmulas de la sexuación presentadas en El Seminario XX.

Ya hemos hecho un recorrido por las distintas referencias lógicas a las que acude Lacan para construir las fórmulas de la sexuación, de manera que en este apartado nos centraremos en la lectura final de las fórmulas.

El aforismo “no hay relación sexual” aparece por primera vez en el seminario 16 dictado entre los años 1968 y 1969 De un otro al otro. Desde ese momento en adelante, asistimos a una proliferación del uso del “no hay relación sexual” en el curso de los seminarios y escritos lacanianos. Las consecuencias de esta formulación para la teoría psicoanalítica son pensadas por Lacan desde otras disciplinas, donde se destaca la lógica, que será imprescindible para en 1973 dar lugar a una de sus más importantes consecuencias: las fórmulas de la sexuación (Le Gaufey, 2014, p. 33) Con la mencionada frase intenta dar cuenta de que no hay proporción sexual, no hay relación entre los sexos. Se trata de una diferencia estructural, un malentendido esencial entre lo masculino y lo femenino, que nos habla de la imposibilidad de la relación. No hay relación sexual en el sentido de que no puede escribirse, y será utilizando a la lógica, como ciencia de lo real, que podemos bordear este imposible.

Lacan afirma que todo ser que habla se inscribe en uno u otro lado de las fórmulas de la sexuación y considera que son las únicas inscripciones posibles. En ambos casos se tiene una relación con la función fálica. El falo actúa, en consecuencia, como el único significante para ambas posiciones en lo que respecta al anudamiento de la sexualidad con el lenguaje. Sin embargo, si bien ambas posiciones mantienen una relación con el falo, la manera de hacer con ella es distinta. Esto queda explicitado en las fórmulas, veámoslo.

El lado izquierdo de las fórmulas es llamado el lado hombre, y el lado de la izquierda corresponde al lado mujer. Comencemos por el lado masculino. Tenemos un primer matema: “Exista un x que no phi de x”, es decir “existe al menos uno que queda por fuera de la función fálica”. Tal como hemos visto con Russell, este al-menos-uno, es el lugar de excepción necesario para dar lugar a un conjunto cerrado. El padre de la horda funda la castración como ley universal, pero él mismo queda exento de la ley, queda por fuera de la función fálica, formándose así un conjunto cerrado y finito porque el límite queda por fuera. Este lugar de excepción es necesario para que sea posible la afirmación del segundo matema: “para todo x phi de x”, es decir “todos quedan en relación a la función fálica”, todos están sometidos a la castración, haciendo conjunto cerrado. Por lo tanto, el matema superior es necesario para que el inferior sea posible.

Por otro lado, del lado femenino tenemos una imposibilidad “no existe un x que no phi de x” (∃x.Φx), es decir “no existe x que no esté sometido a la función fálica”. Al no dar lugar a una excepción, impide un decir universal, de ahí la imposibilidad de un “para todos” en la escritura de la posición femenina y en su lugar encontramos el invento de Lacan: el “no-todo” (∀x). Poner la barra sobre el cuantificador es lo imposible de escribir lógicamente y es así como el no-todo permite dar cuenta de lo indecible (bordear ese imposible de escribir).

Con el “no-todo” Lacan se distancia de la lógica aristotélica al poner la barra sobre el cuantificador mismo. Para el filósofo griego, la negación de un universal tiene como consecuencia un universal de signo contrario. Es decir, al negar un universal positivo obtenemos un universal negativo y viceversa. Por ejemplo, la negación de “Todo X es Y” es que “ningún X es Y” y la negación de que “Ningún X es Y” es que “Todo X es Y”. Sin embargo, al negar el cuantificador, Lacan abre una posibilidad distinta de la de pasar de un universal a otro en favor de un “no todo”, ya no se tratará de una universal negada (Lacan, 2012, p. 14). Remitiéndonos a la fórmula (∀x.Φx) tendremos dos posibilidades: Fx y no Fx. Por lo tanto, a diferencia de Aristóteles, no estamos ante un mismo valor de signo contrario (un “todo” o un “ningún”) sino que, negando el cuantificador “para todo” obtenemos la apertura de dos valores distintos y que pueden coincidir al mismo tiempo. Acá podemos leer la influencia de Peirce y la forma de entender la proposición particular en sentido máximo: “algunos, pero no todos”. Es en esta dirección que debemos leer la fórmula “no todo x phi de x” donde por un lado la función fálica está activada y por otro no. Ya no se trata de o está activada o no lo está, sino que ambas opciones son posibles (Lacan, 2012, pp. 43-46). De aquí que, en la mujer no todo el goce está regido por la función fálica. Hay algo en la mujer que se rige por la función fálica, pero no todo. También hay un goce Otro, un goce complementario, que no se puede decir ni localizar.

En este caso lo imposible “no existe x que no phi de x” da lugar a lo contingente “no para todo x phi de x”, no todos están inscriptos en la función fálica. Leemos este matema desde la perspectiva de la contingencia entendiéndola como es posible que “x phi de x” pero también que “x no phi de x”. La inexistencia de la excepción para fundar el todo, da lugar a un conjunto abierto, infinito: el de las mujeres. Teniendo en cuenta esto, termina de cobrar sentido la frase de Lacan “La mujer no existe”, pues la falta de un lugar de excepción implica el no poder formar clase.

Si bien Lacan habla de la posición hombre y la posición mujer, cualquiera sea su sexo biológico, los seres hablantes pueden ubicarse de uno u otro lado de las fórmulas. En lo que refiere al goce, para todo x, sea quien sea, tendrá que vérselas con la castración Φ. Como hemos visto en este punto, Lacan se basa en el concepto de función de Frege, para pensar la sexuación desde un lugar no ligado a la biología. Todo ser hablante, si se inscribe la castración, se las verá con la discordancia de los sexos.

Conclusiones

Podemos considerar que las fórmulas de la sexuación son uno de los desarrollos más complejos de Lacan. En este capítulo nos limitamos a realizar una aproximación a las referencias lógicas en la construcción de las fórmulas, y no nos referimos a las consecuencias clínicas ni a las consecuencias teóricas que tienen dentro de la obra de Lacan. A la vez, se trata de un recorte, ya que hicimos un recorrido por los Seminarios 18, 19 y 20, pero este análisis podría continuarse por medio de la lectura de algunos escritos, como es el caso del El Atolondradicho (1973) contemporáneo al Seminario 19 y considerado el más difícil de los escritos de Lacan. En este texto, el autor continúa con las consecuencias del enunciado “no hay relación sexual” para el discurso analítico.

El objetivo ha sido mostrar los diálogos que Lacan ha tenido con la lógica y cómo la ha utilizado para construir algunas de sus herramientas teóricas. De esta manera, queda claro que no podemos escindir la obra de Lacan del momento histórico del pensamiento filosófico y lógico matemático, ya que los desarrollos y controversias que se estaban dando en la lógica atravesaron la obra de Lacan. Sin embargo, resulta llamativo que más allá de las numerosas referencias a lógicos como Aristóteles, Frege, Russell, Gödel, Cantor, Boole y De Morgan, Lacan utiliza los conceptos lógicos con un sentido muy distinto al que se les dio en su campo de origen.

Esta parece ser una característica del pensamiento lacaniano ya que lo mismo sucede con el uso que hace de la lingüística. Él mismo sostiene:

Dado que la lingüística hoy fue mi eje, les diré que, siempre que la lingüística sea convenientemente filtrada, criticada, focalizada, en fin, para decirlo todo, siempre que hagamos exactamente lo que queremos con lo que hacen los lingüistas, Dios mío, ¿por qué no sacarle provecho? (Lacan, 2009, p. 49)

Esto sucede con varias de las referencias extra- psicoanalíticas: Lacan exporta conceptos de otras disciplinas y los reformula en función de la teoría psicoanalítica. Por consiguiente, al leer la obra de Lacan debemos estar advertidos que cuando toma conceptos de la lógica, lo hará en la mayoría de los casos dándoles su propio sentido.

Bibliografía

Fernández Guilañá, E. (2017): Aproximación lógica a las fórmulas de la sexuación. NODVS XLVIII.

Frege, G. (1998): Función y concepto [1891], en Frege, G. (1998): Ensayos de semántica y filosofía de la lógica, Edición, introducción, traducción y notas de Luis M. Valdés Villanueva Tecnos, Madrid.

Freud, S. (1913): Tótem y tabú. Algunas concordancias en la vida anímica de los salvajes y de los neuróticos, Amorrortu Ediciones, tomo XIII.

Gutiérrez Arconada, J.M. (2023): La Vía Lógica en Jacques Lacan, Tesis Doctoral, Universidad Complutense de Madrid, Facultad de Filosofía.

Iuale, L. (2017): La construcción de las fórmulas de la sexuación, Facultad de Psicología UBA, Revista Universitaria de Psicoanálisis (2017, N°17) pp. 107-114, ISSN 1515-3894.

Lacan, J. (1964-1965) Seminario Libro 12: Problemas cruciales del psicoanálisis (inédito).

Lacan, J. (2004): El Seminario 20 Aún (1972-1973), Buenos Aires, Paidós.

Lacan, J. (2007 [1975]): Quizás en Vincennes…, en Lacan, J (2007): Otros escritos, Buenos Aires, Paidós, pp. 333-335.

Lacan, J. (2009): El Seminario 18 De un discurso que no fuera del semblante (1971), Buenos Aires, Paidós.

Lacan, J. (2012): El Seminario 19: … o peor (1971-1972), Buenos Aires, Paidós.

Le Gaufey, G. (2007): El notodo de Lacan: consistencia lógica, consecuencias clínicas, Buenos Aires, El cuenco de plata.

Le Gaufey, G. (2014): Hiatus sexuales. La no relación sexual según Lacan, El cuenco de Plata.

Peirce, C.S. (2003 [1893]):  “La silogística aristotélica”. Traducción castellana de Sara Barrena. Texto digital: https://www.unav.es/gep/SilogisticaAristotelica.html

Roudinesco, E. (1993). La batalla de cien años. Historia del psicoanálisis en Francia (1925-1985). Tomo 2. Madrid: Fundamentos.

---