Importancia y estrategias

Daniel Busdygan

… mencioné la esperanza decimonónica de que, tal como rezaba una fórmula, la lógica se redujera a una “física del pensamiento”. A ese proyecto le siguió un enfoque reflejado en otra fórmula, de acuerdo con la cual la lógica es en realidad una “ética del pensamiento”, no nos dice cómo razonamos, sino cómo debemos razonar, e indica una manera de responder a la pregunta que hemos planteado a los teóricos de la virtud: ¿cómo podríamos los seres humanos tomar en serio un ideal tan inalcanzable? […] Podemos, inspirarnos, entonces, en la esfera del razonamiento inductivo y deductivo, donde también aspiramos a ideales inalcanzables, pero en la que al menos entendemos (no a la perfección, pero mucho mejor) cómo se vincula un ideal inalcanzable con la práctica real.

   

Kwame Appiah, Experimentos de ética

Deducción natural y la relevancia del enfoque sintáctico en la enseñanza de la lógica

En la enseñanza de la lógica formal, una de las cuestiones centrales no es únicamente qué reglas permiten derivar una fórmula desde un conjunto de premisas sino cómo se forma un razonador capaz de comprender, justificar y aplicar correctamente esas reglas en contextos diversos. Si bien para muchos, enseñar deducción natural puede consistir simplemente en transmitir un algoritmo o una técnica operativa, a nuestro juicio, debería consistir en formar una práctica intelectual en la que se aprende a distinguir con rigor entre suposiciones legítimas, consecuencias lógicas y pasos inferenciales válidos. En este sentido, el sistema de deducción natural representa algo más que un conjunto de procedimientos formales: es un modelo normativo del razonamiento, una herramienta que permite hacer explícitas las condiciones bajo las cuales una conclusión puede decirse justificada desde ciertas premisas.

El desafío didáctico que plantea este sistema radica en enseñar a los estudiantes no tanto a “hacer deducciones” como si se tratara de una receta sino a reconocer el carácter constructivo, normativo y estratégico de una derivación. Esto implica comprender cuándo y por qué introducir un supuesto auxiliar, cómo anticipar la regla que permitirá cerrar una deducción auxiliar, o por qué la elección de una constante no puede ser arbitraria en cualquier contexto. Así, cada regla formal aparece anclada en una forma de ‘responsabilidad’ inferencial que excede la mera manipulación simbólica. Las páginas que siguen se organizan como una aproximación progresiva a esta práctica, alternando presentaciones formales de las reglas del sistema con ejemplos, errores comunes y comentarios estratégicos. En este recorrido, no se trata sólo de alcanzar conclusiones sino de formar una mirada lógica sobre el camino que conduce hasta ellas.

Uno de los desafíos recurrentes en la lógica formal es lograr que los estudiantes no memoricen reglas abstractas sino que comprendan y experimenten cómo opera la inferencia lógica en contextos concretos. En ese sentido, la deducción natural constituye una herramienta particularmente valiosa tanto por su estructura formal como por su cercanía con las prácticas argumentativas del lenguaje ordinario. La incorporación de la deducción natural en los cursos de lógica suele estar condicionada por limitaciones estructurales que no son exclusivamente conceptuales. En muchos programas, la lógica proposicional y la lógica de predicados deben ser abordadas en tiempos acotados, lo que obliga a seleccionar, dosificar y jerarquizar contenidos en función de criterios didácticos y curriculares. En ese contexto, la presentación del sistema de deducción natural aparece muchas veces relegada a los tramos finales del curso, cuando el calendario académico ya impone restricciones para su apropiación gradual.

Esta situación plantea un doble desafío. Por un lado, implica enseñar un aparato formal complejo en condiciones que no siempre permiten la ejercitación sostenida que requiere su dominio. Por otro lado —y más profundamente—, invita a revisar qué tipo de lógica se enseña cuando se opta por modelos normativos del razonamiento y qué lugar queda, en ese marco, para las aproximaciones descriptivas que provienen de la psicología del razonamiento. Por consiguiente, el hecho de comprender cómo se razona efectivamente, con qué sesgos, heurísticas o atajos cognitivos, constituye una dimensión fundamental para una formación lógica integral (Daguerre y Elgarte, 2018), aunque muchas veces quede excluida de los programas clásicos.

La deducción natural, en este sentido, no sólo debe ser presentada como una técnica para derivar fórmulas sino también como un punto de cruce entre la lógica como disciplina normativa y el estudio empírico del razonamiento humano. Idealmente, los cursos de lógica deberían reservar un espacio para que estas dos perspectivas entren en diálogo—la normatividad formal y la descripción cognitiva—, permitiendo así una reflexión más amplia sobre qué significa razonar, qué errores cometemos al hacerlo y cómo una lógica bien enseñada puede colaborar en la formación de prácticas racionales críticas y conscientes.

Habiendo dejado sentadas las bases en que se inscribe esta reflexión, podemos concentrarnos en su tratamiento. En términos generales, la deducción natural es un método formal para derivar conclusiones a partir de premisas mediante reglas de inferencia claramente definidas. A diferencia de sistemas axiomáticos clásicos, el sistema de deducción natural se caracteriza por su enfoque intuitivo, cercano al razonamiento humano cuando este lo hace correctamente. Esta cercanía está dada porque permite trabajar con suposiciones temporales y presenta una estructura de demostraciones de manera jerárquica donde se explicita cómo una fórmula se sigue de otra y cuál es la regla que justifica ese paso inferencial. En otras palabras, se trata de un tipo de cálculo perteneciente a la familia de los llamados cálculos tipo Gentzen. Veamos brevemente este punto.

Alonso (2011) distingue entre dos clases fundamentales de sistemas deductivos: por un lado, los cálculos tipo Hilbert, también llamados sistemas axiomáticos que se organizan a partir de un conjunto fijo de axiomas y un repertorio de reglas de inferencia aplicables sobre dichos axiomas o sobre fórmulas ya derivadas de ellos; y, por otro lado, los cálculos tipo Gentzen que prescinden de axiomas y se estructuran exclusivamente en torno a reglas de transformación orientadas a la manipulación sintáctica directa de fórmulas, ya sea en forma de deducción, tablas o secuentes (Alonso, 2011, pp. 89–90). Dentro de la familia de cálculos gentzenianos se inscribe el llamado cálculo de deducción natural y su relevancia excede los límites del tratamiento puramente formal puesto que puede proyectarse hacia el análisis de la inferencia en el lenguaje ordinario. Así, los sistemas del tipo Gentzen permiten derivar teoremas a partir de un conjunto vacío de fórmulas como también permiten establecer conclusiones a partir de conjuntos arbitrarios de fórmulas (Alonso, 2011, p. 90). En lugar de partir de verdades establecidas a priori, como en los sistemas axiomáticos, la deducción natural trabaja con supuestos que pueden introducirse y eliminarse dentro del desarrollo de una derivación, siguiendo un principio de construcción progresiva y contextualizada de la inferencia. Fue desarrollada en la década de 1930 por lógicos como Gerhard Gentzen y Stanisław Jaśkowski con el objetivo de reflejar cómo las personas construyen argumentos en contextos matemáticos que luego se extienden a otros.

La estructura básica de este cálculo deductivo se apoya en reglas de introducción y eliminación para cada conectiva lógica. Veremos las reglas más abajo, no obstante, solo por poner un ejemplo, la regla de introducción de la conjunción (∧) permite derivar A ∧ B si se ha afirmado previamente A y B por separado; la eliminación de la conjunción permite pasar de A ∧ B a cualquiera de sus componentes. Este modo de proceder se replica para otras expresiones lógicas como la disyunción (∨), el condicional (→), la negación (¬) y los cuantificadores que se incorporan en la lógica de primer orden, universal (∀) y existencial (∃). Así, a través de reglas explicitadas se constituye un sistema que busca hacer también explícitas las operaciones inferenciales fundamentales del razonamiento deductivo.

Desde el punto de vista didáctico, este sistema tiene la ventaja de permitirles a los estudiantes visualizar de manera clara cómo se construye una derivación a partir de supuestos iniciales, premisas, y cómo cada paso de la cadena derivativa debe estar justificado por una regla explícita del sistema. Esto convierte a la deducción natural en una herramienta pedagógica relevante en tanto: (i) no exige memorizar axiomas abstractos; (ii) como tampoco aplicar transformaciones opacas. Por el contrario, (iii) permite seguir el hilo argumental de la inferencia paso a paso y evita que se den tanto errores o falacias como saltos injustificados; (iii) modela cómo trabajar con suposiciones y descartarlas- por ejemplo, con deducciones auxiliares de reducción al absurdo-, y con ello ejercita la capacidad de evaluar hipótesis y sus consecuencias.

Otra virtud central de este enfoque radica en: (iv) su capacidad para captar la dimensión constructiva del razonamiento lógico; permite ver cómo, a partir de ciertos enunciados dados, puede derivarse legítimamente una conclusión u otra/s proposición/es. Esta estructura busca reflejar, con mayor fidelidad, la dinámica real del razonamiento humano: partimos de datos dados, premisas, y buscamos argumentar en secuencias justificadas para extraer conclusiones en función del curso de la inferencia. Cuando nos proponemos desarrollar cierta conciencia normativa donde cada paso de una derivación esté debidamente justificado por una regla explícita, comprensible y accesible, la deducción natural nos permite representar el razonamiento como una construcción progresiva y controlada en la que la validez de cada paso se define por su forma lógica más que por intuiciones informales.

Asimismo, esta perspectiva también tiene un valor formativo profundo porque invita al estudiante a internalizar las reglas que gobiernan la inferencia correcta más que a evaluar resultados desde afuera, desde un punto de vista externo. Está claro también que la internalización de reglas evita o impide que se internalicen errores frecuentes, por ejemplo, la regla de la eliminación del condicional o modus ponens, impediría la confusión con la falacia de la afirmación del consecuente (Nisbett, 2016). Desde una perspectiva didáctica, este enfoque tiene un valor excepcional. Si bien proporciona herramientas técnicas es también un modelo normativo del razonamiento. En su análisis de las reglas de inferencia, Marraud (2011) enfatiza que estas no deben entenderse como simples mecanismos de transformación simbólica sino como dispositivos que orientan la corrección de los pasos inferenciales dentro de una práctica discursiva. La lógica, en este sentido, no sólo formaliza relaciones, sino que prescribe formas legítimas de pasar de unas proposiciones a otras (Marraud, 2011, p. 187 y ss.), lo cual refuerza su valor formativo en la enseñanza de la argumentación.

Alcances y limitaciones

La importancia del cálculo de deducción natural tanto para aquellos que se forman en la filosofía como quienes lo hacen en el derecho, radica en su capacidad de ofrecer un modelo formal del razonamiento que, por un lado, clarifica los criterios de validez en el discurso argumentativo y, por otro, permite estructurar con rigor las justificaciones que se producen en ámbitos normativos. Si bien esta relevancia epistemológica y práctica se manifiesta de manera distinta en cada disciplina, comparte un fundamento común, a saber: la necesidad de contar con procedimientos explícitos que orienten la evaluación racional de las inferencias.

Desde la perspectiva filosófica, la deducción natural constituye una herramienta central para el análisis lógico de los argumentos en tanto permite representar de manera sistemática la transición de premisas a conclusiones. A diferencia de otros sistemas, su estructura proporciona un marco más intuitivo y flexible en el que se hace posible reconstruir con precisión la forma lógica de razonamientos complejos. Allí, si bien la función es descriptiva, también es regulativa: orienta la corrección inferencial lo cual es esencial para toda práctica filosófica comprometida con la claridad conceptual y la coherencia lógica.

En el ámbito jurídico, la deducción natural adquiere un valor metodológico particular en la medida en que permite clarificar la estructura interna de las argumentaciones normativas. El razonamiento jurídico no se agota en la mera aplicación mecánica de normas, pues requiere justificar las decisiones a través de cadenas inferenciales que conecten principios, reglas y hechos relevantes del caso. En ese contexto, la deducción natural ofrece un modelo formal útil para reconstruir la validez de dichos razonamientos, ya sea en el plano doctrinal, jurisprudencial o constitucional. Por ejemplo, al analizar una sentencia, puede preguntarse si la conclusión (el fallo) se sigue de manera válida de las normas aplicadas y de la interpretación adoptada de los hechos, si se ha probado lo que concluye, lo cual supone —al menos idealmente— un recorrido inferencial normativamente controlado. Más aún, permite formalizar no sólo derivaciones desde normas a consecuencias, además puede revisar las relaciones entre las proposiciones normativas mismas, lo que resulta relevante para debates sobre coherencia normativa, lagunas del sistema o conflictos de normas. La posibilidad de representar con claridad la estructura inferencial de una decisión contribuye a la transparencia del razonamiento judicial, lo cual es un requisito básico del principio republicano de publicidad y del ideal deliberativo de racionalidad pública. Así, lejos de pensar que su valor reside únicamente en su formalismo, puede verse su capacidad para articular prácticas de justificación racional mediante reglas explícitas, públicas y replicables, condiciones todas ellas necesarias tanto para la crítica filosófica como para la legitimidad jurídica.

Una de las limitaciones más relevantes de este sistema que está dentro del enfoque sintáctico de la enseñanza de la lógica radica en que su dominio técnico, por sí solo, no garantiza una mejora efectiva en las capacidades reales de razonamiento. En otros términos, muchos de aquellos que pasaron por un curso de lógica y aprendieron solo eso, es probable que puedan hacer complejas deducciones con una larga cadena de pasos pero fallen al responder sobre problemas simples como el de la pelota y la paleta que plantea Kahneman (2011).^[1] Aunque estos sistemas formales proporcionan un modelo riguroso, su aplicación está limitada a contextos ideales de razonamiento controlado. De modo que, la lógica formal especifica condiciones de corrección pero no explica cómo efectivamente razonan los seres humanos la mayor parte de las veces en contextos cotidianos, donde el tiempo es escaso, la información incompleta y los recursos cognitivos son limitados. En este sentido, es fundamental reconocer que el desarrollo de competencias en lógica formal no implica automáticamente que las personas razonen mejor fuera de ese dominio técnico. Alguien puede ser capaz de identificar una deducción correcta en un entorno estructurado y, sin embargo, incurrir en razonamientos falaces en situaciones reales, afectado por sesgos cognitivos, prejuicios o inferencias apresuradas.

La existencia de esta brecha entre conocimiento normativo y desempeño práctico ha sido ampliamente investigada desde la década del setenta por Daniel Kahneman y Amos Tversky. Desde su perspectiva, el razonamiento humano se estructura según un modelo de sistemas. El Sistema 1 opera de forma rápida, intuitiva, automática y, en muchos casos, efectiva. El Sistema 2, en cambio, es lento, deliberativo, analítico y controlado. Ahora bien, aunque la lógica formal se asocia típicamente con el funcionamiento del Sistema 2, la mayor parte de nuestras inferencias cotidianas son producidas por el Sistema 1. El Sistema 1 se basa en heurísticas, atajos mentales evolutivamente adquiridos que permiten tomar decisiones sin procesar exhaustivamente toda la información disponible. Estas heurísticas pueden resultar eficaces en ciertos contextos pero también generan distorsiones sistemáticas en el razonamiento, conocidas como sesgos cognitivos.^[2] Por este motivo, es insuficiente asumir que el entrenamiento en deducción formal basta para formar razonadores más competentes. Si bien el conocimiento de reglas de inferencia es necesario para evaluar la corrección de los argumentos, este saber debe complementarse con una comprensión de cómo y por qué las personas se desvían de esos modelos normativos.

El estudio de las heurísticas y de los sesgos no pretende sustituir a la lógica formal sino ampliar el enfoque en tanto muestra cuándo los mecanismos intuitivos producen respuestas racionales, y cuándo, por el contrario, conducen a errores previsibles. Mientras la lógica formal proporciona los estándares ideales de inferencia, la psicología del razonamiento permite diagnosticar las condiciones bajo las cuales los seres humanos efectivamente se ajustan —o se desvían— de tales estándares.

Por consiguiente, una concepción más integral de la racionalidad debe incluir tanto el análisis formal de la validez como el estudio empírico del comportamiento inferencial real. En lugar de contraponer lógica y psicología, es más fructífero entenderlas como perspectivas complementarias. De esa forma, se hace posible una formación que, a la vez, enseña cómo deberían hacerse las inferencias, cómo efectivamente se hacen, y qué puede hacerse para mejorar ese desempeño.

En lo que sigue, nos detendremos en la presentación del cálculo de deducción natural, sus reglas fundamentales y algunas estrategias que pueden facilitar la resolución de derivaciones. El desarrollo de estas estrategias responde a una concepción de la enseñanza de la lógica centrada en la formación de la capacidad inferencial más que en la mera reproducción de soluciones. En este marco, la tarea del docente no consiste en resolver por el estudiante sino en enseñarle a resolver; no se trata de mostrar que la deducción es propiedad de las competencias del docente sino de hacer explícito cómo se construye una derivación, qué aspectos conviene observar, cómo se piensan los supuestos, dónde es posible encontrar indicios relevantes para avanzar y qué preguntas formularse cuando la prueba se vuelve compleja o no avanza. Así entendida, la enseñanza de la lógica se orienta a formar una mirada activa y estratégica sobre el razonamiento más allá del dominio mecánico de las reglas.

Deducción natural

Cuando aceptamos que razonar no consiste meramente en transitar de unas proposiciones a otras, sino que debemos justificar esos pasajes conforme a reglas normativas, entonces, allí surge una pregunta central: ¿qué condiciones debe cumplir una regla para ser considerada lógicamente válida? ¿Toda regla que preserva la verdad es admisible y prescribe la inferencia? Esta sección se propone examinar esos criterios como principios que guían la enseñanza de la deducción natural. A nuestro juicio, enseñar a aplicar una regla no es simplemente mostrar su funcionamiento técnico, es sobre todo habilitar la comprensión de por qué puede (y debe) usarse en determinadas condiciones y no en otras.

La noción de deducibilidad es una noción sintáctica, por cuanto sólo queda especificada por reglas de inferencia que determinan qué fórmulas pueden ser obtenidas a partir de otras, independientemente de cuál fuere el valor de verdad. El enfoque sintáctico se desarrolló en la búsqueda por construir un lenguaje matemático en el que se recobren aspectos formales relegando y hasta prescindiendo de los significados y de los valores de verdad (Palau, 2002, p. 43). En este enfoque la noción de validez está ligada al hecho de si una fórmula es deducible a partir de un conjunto de fórmulas mediante reglas propias del sistema. La noción de deducibilidad la podemos expresar de las siguientes formas:

Para el conjunto Γ y la fórmula ψ se cumple que:

Γ├ ψ, si existe una derivación de ψ a partir de Γ^[3]

Una presentación similar pero sin considerar las fórmulas como un conjunto puede establecerse de la siguiente manera. Para las fórmulas φ₁… φ_n y ψ, se cumple que:

φ₁… φ_n ├ ψ, si existe una derivación de ψ a partir de φ₁…φ_n. ^[4]

Bien, desde una perspectiva instrumental en la que dejamos de lado las consideraciones semánticas, ψ es una consecuencia sintáctica si a partir de Φ₁…… Φ_n y por medio de reglas aceptadas se puede hallar una derivación.

1.   Φ     Premisa. supuesto inicial

       ⁞

m.  ψ   O bien se obtuvo a partir de la fórmula anterior
            o bien es un supuesto auxiliar.

n.   χ    Última fórmula de la derivación. Conclusión.

Si un argumento es válido, entonces existe al menos una derivación posible de las premisas que nos llevan a una fórmula bien formada (fbf) que entenderemos como la conclusión, por medio de “principios lógicos aceptados previamente” (Legris, 2001, p. 6)

Φ₁…Φ_i Ⱶ Φ_n “y decimos: existe una derivación de Φ_n a partir de (los supuestos) Φ₁…Φ_i”. (Gamut, 2002, p. 136)

Un razonamiento es válido si hay una derivación de su conclusión a partir de las premisas aplicando principios lógicos; si existe esa derivación, entonces puede entenderse como una demostración o prueba (proof) (Legris, 2001). Cada paso de la deducción forma una cadena formal que liga premisas y conclusión con reglas que, si por caso, las premisas fueran verdaderas, las reglas mantienen, aseguran, preservan o heredan ese valor de verdad verdadero a las nuevas fórmulas que se generan. Dado un argumento válido cualquiera, el modo sintáctico de demostrarlo consiste en obtener la conclusión deseada a partir de las premisas, por medio de las reglas de inferencias (i.e., pequeños razonamientos correctos y en algunos casos triviales). Este enfoque da cuenta del significado de las conectivas y los cuantificadores desde un plano meramente instrumental quedando reducidos a procedimientos calculísticos (Quesada, 1995, p. 95).

Ahora bien, del mismo modo que entendemos la deducción como un procedimiento que permite demostrar la validez formal de un razonamiento, debemos advertir que la imposibilidad de llevar a cabo tal demostración no implica, en sentido estricto, que el argumento considerado sea lógicamente inválido. Cabe la posibilidad de que el razonamiento sea formalmente válido aunque no logremos construir su prueba debido a limitaciones cognitivas, falta de familiaridad con las estrategias deductivas pertinentes o simplemente porque el camino inferencial adecuado no se nos presenta con claridad en ese momento. Por otro lado, si el argumento fuese efectivamente inválido —es decir, si su conclusión no se siguiese lógicamente de las premisas—, entonces ningún procedimiento deductivo legítimo podría conducir a una demostración. En tal caso, la imposibilidad de deducir no sería contingente sino necesaria dado que no existe una derivación válida posible.

Recordemos que un sistema lógico se considera decidible cuando existe un algoritmo, es decir, un procedimiento efectivo y finito que permite determinar, para cualquier fórmula dada, si esta es o no deducible en dicho sistema. En relación con esta noción, el llamado teorema de Church establece que la lógica de predicados de primer orden (LPO), en su forma general, es indecidible. Esto significa que no existe un algoritmo que permita resolver de manera sistemática y en todos los casos si una fórmula arbitraria del lenguaje es deducible o, en términos equivalentes, si un determinado esquema argumentativo es formalmente válido. Dicho de otro modo, para los argumentos inválidos formulados en el marco de LPO no contamos con un procedimiento general que nos garantice la detección efectiva de su invalidez. Esta indecidibilidad afecta particularmente a aquellas fórmulas que contienen predicados poliádicos, es decir, de aridad mayor que uno. En cambio, si restringimos el lenguaje a fórmulas que emplean exclusivamente predicados monádicos –de aridad uno–, el sistema resulta decidible: en ese fragmento de la LPO sí es posible construir un algoritmo que determine la validez o invalidez de cualquier fórmula.

Esta distinción entre fragmentos decidibles e indecidibles de LPO permite comprender que la indecidibilidad no es una propiedad homogénea del sistema completo sino que afecta selectivamente a ciertas configuraciones estructurales del lenguaje. Por ello, aunque la LPO en su totalidad sea indecidible, algunos de sus sublenguajes sí permiten procedimientos de decisión completos.

Recordemos algo más: una derivación se define como una secuencia finita de fórmulas bien formadas (en adelante, fbf), cada una de las cuales está numerada con un número natural que indica su posición en la serie. En esta secuencia, cada fórmula puede ocupar uno de dos lugares: o bien se trata de un supuesto —ya sea inicial o auxiliar—, o bien ha sido obtenida a partir de fórmulas precedentes mediante la aplicación de alguna regla de inferencia reconocida por el sistema.

En el caso de los supuestos auxiliares, su condición particular se señala gráficamente mediante la apertura de una caja o llave, que delimita el ámbito de validez local de dicho supuesto. Ese recurso permite introducir una hipótesis de trabajo que deberá, eventualmente, ser cancelada o cerrada al concluir el razonamiento dentro de ese subespacio deductivo. Por contraste, los supuestos iniciales no están sujetos a cancelación, ya que constituyen las premisas permanentes de la derivación.

En consecuencia, si en el transcurso de una derivación aparece alguna fbf que no ha sido obtenida por regla ni figura como supuesto, tal fórmula constituye una anomalía estructural: o bien se trata de una premisa legítima que no ha sido debidamente registrada como tal, o bien es un supuesto auxiliar que, si no se cancela adecuadamente, invalida la obtención correcta de la conclusión. Toda derivación completa debe concluir con una fbf que represente la conclusión del razonamiento, y que esté justificada únicamente por supuestos debidamente introducidos y, en su caso, cancelados conforme a las reglas del sistema.

Sobre las reglas del sistema de deducción natural (SDN)

Toda forma lógica válida de un razonamiento puede ser tomada como una regla de inferencia o regla lógica. En este sentido, su condición de regla prescribiría la manera en que estamos obligados a seguir una conclusión de la aceptación de determinadas premisas. Por tanto, en la aplicación de una regla lógica estamos deduciendo un enunciado de otro/s.

Las reglas básicas del SDN de Gentzen, se proponen como reglas de inferencias y en ese sentido deberían destacarse dos puntos:

1. se centran en el concepto de argumento válido y no en teoremas o verdades lógicas como lo hacían los sistemas axiomáticos y
2. buscan realizar en la deducción la misma naturalidad que pueden experimentarse en las inferencias del pensamiento natural. (Palau, 2002, p. 30)

Es así que estas reglas se establecen como un conjunto finito de reglas básicas con las cuales se permitiría la transformación de una fórmula de LPO a otra fórmula; además, mediante estas reglas del SDN también consideraremos a otras fórmulas como supuestos. Estas reglas de inferencia son “pequeños pasos para formar derivaciones” (Gamut, 2002, p. 135). En consecuencia, “la inferencia deductiva tiene la peculiaridad de ser una inferencia necesaria en el sentido de que hace forzosa la aceptación del enunciado inferido a partir de otros enunciados ya aceptados” (Legris, 2001, p.3). Cada una de las reglas que constituye el SDN, es una forma válida de razonamiento –un pequeño argumento correcto, de modo que si la fórmula a la que se le aplica esa regla fuese verdadera, entonces las fórmulas que derivemos también lo serán. No obstante, es característico del SDN no presuponer un valor de verdad a las constantes lógicas que intervienen.

A modo de resumen podemos exponer que los rasgos que caracterizan al SDN, según la filósofa Gladys Palau (2002, p. 30) son:

1. las reglas de inferencia son reglas de derivación mediante las cuales podemos mostrar la validez de inferencias. Esto significa que no fueron originalmente pensadas para la demostración de la teoremicidad de determinadas fórmulas;
2. existen dos clases de supuestos, por lado, las premisas o supuestos iniciales y por otro, los supuestos auxiliares o adicionales. No hay axiomas;
3. las reglas que cuentan con la introducción de supuestos auxiliares tienen como deber cancelarlos o descargarlos. Por otro lado, no es obligatorio cancelar los supuestos iniciales o premisas;
4. un teorema es una deducción a partir de un conjunto vacío de supuestos;
5. “el significado de las constantes lógicas se fija por medio de las reglas que determinan su uso en el cálculo (i.e., reglas de inferencia); y
6. una derivación (o deducción) es una sucesión finita de fórmulas donde cada una es o un supuesto inicial, o un supuesto adicional o una consecuencia lógica de anteriores aplicaciones de una de las reglas de inferencia del cálculo” (Ibídem, énfasis añadido)

El SDN tiene reglas de introducción (en adelante, I) y de eliminación (en adelante, E) para las conectivas y para los cuantificadores, además de reglas adicionales como la eliminación de la doble negación ((E¬¬) y una regla que se deriva de esa, la regla ex falso sequitur quodlibet (EFSQ). Estas reglas del SDN son las mismas para el sistema de la Lógica proposicional (LP). Cada una de las conectivas cuenta con una regla de introducción y otra de eliminación, estableciendo cómo realizar correctamente cada una de estas acciones en una derivación. Presentemos las reglas de SDN de Gentzen respectivas a las conectivas.

Reglas para la conjunción^[5]

Reglas para el condicional

Reglas para la disyunción

Reglas para la negación y el EFSQ

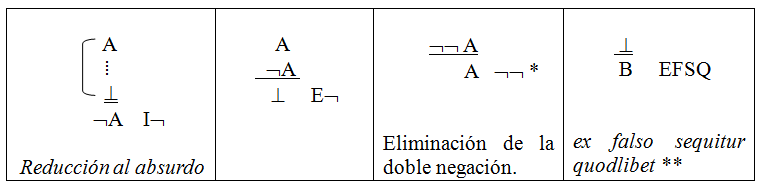
* La regla de eliminación de la doble negación no se deduce de manera trivial a partir de las reglas de introducción y eliminación de las demás conectivas, razón por la cual debe ser incorporada de manera independiente si se pretende que el sistema refleje fielmente todas las leyes de la lógica clásica de primer orden. Su inclusión, en este sentido, no es opcional si se aspira a garantizar que el sistema sea deductivamente completo respecto del conjunto de tautologías clásicas. Por ejemplo, sin esta regla, no podría demostrarse la validez del principio del terso excluso (A ∨ ¬A), el cual constituye uno de los axiomas fundamentales de la lógica clásica. Esta cuestión delimita con claridad una frontera doctrinal entre los sistemas clásicos y los sistemas intuicionistas. Desde la perspectiva intuicionista, la doble negación de una fórmula no equivale, ni ontológica ni epistémicamente, a su afirmación directa. En consecuencia, se rechaza tanto la validez de la eliminación de la doble negación como la derivabilidad del principio del terso excluso. Este rechazo da lugar a una lógica de naturaleza constructivista, divergente en su fundamento respecto del paradigma clásico, y con implicancias filosóficas sustantivas sobre la noción misma de verdad, prueba y significado lógico (Palau, 2002, C. 3).

** La conformación de un sistema de deducción natural no está exenta de decisiones controvertidas en torno a qué reglas de inferencia deben ser admitidas. En particular, una de las más discutidas —tanto por su potencial alcance como por su aparente carácter contraintuitivo— es la regla conocida como ex falso sequitur quodlibet (EFSQ), que permite derivar cualquier fórmula a partir de una contradicción explícita. Esta regla, si bien derivable en muchos sistemas, ha sido objeto de críticas por quienes consideran que la validez de inferir arbitrariamente desde una contradicción no refleja el modo en que razonamos en contextos naturales o normativos. Cabe señalar que EFSQ no suele figurar como una regla primitiva independiente, sino que se deriva como consecuencia de aceptar otras reglas estructurales del sistema, en particular la eliminación de la doble negación (¬¬A ⊢ A). Dicha regla, que también ha sido objeto de controversia, permite restituir la afirmación de una fórmula a partir de la negación de su negación, y representa un rasgo distintivo de la lógica clásica frente a enfoques no clásicos como el intuicionismo. En efecto, una vez que se admite la eliminación de la doble negación como regla válida, se sigue de manera indirecta la validez de EFSQ, de modo que esta última puede considerarse, en cierto sentido, una regla subsidiaria o derivada dentro del marco deductivo de la lógica clásica; su función es completar un sistema que se adecúe a un reflejo completo de la lógica clásica de primer orden. Si no se contase con esa regla, no podría demostrarse tampoco la tautología terso excluso (GAMUT, 2002, p. 148 y ss.).

Ejercicios

El propósito didáctico de los ejercicios que se presentan a continuación es fomentar la articulación inicial entre dos competencias fundamentales en el aprendizaje de la lógica formal: por un lado, la simbolización precisa de razonamientos válidos en lenguaje formal; por otro, su demostración rigurosa mediante el sistema de deducción natural. El desarrollo de esta doble habilidad —representar estructuralmente un argumento y justificar su validez a través de una secuencia inferencial normativa— constituye un paso esencial en la formación del pensamiento lógico. Se invita, por tanto, a abordar cada ejercicio como una instancia de análisis, traducción y construcción deductiva, orientada a consolidar la comprensión del vínculo entre forma lógica y validez inferencial.

Consignas

1. traduzca el siguiente argumento válido a LPO y efectúe la correspondiente derivación a partir de las reglas del SDN.

Si Gustavo es mayor que Carlos, eso implica que Carlos no es ingresante. Pero Carlos es ingresante. De modo que Gustavo no es mayor que Carlos.

* En adelante pondré el símbolo lógico por el cual fue introducido el supuesto. Esta notación puede aclararse a los alumnos que no es convencionalmente necesaria, pero aquí se justifica por fines estrictamente didácticos. Se debe comprender que la instalación de supuestos en una derivación siempre responde a una estrategia por aplicar una regla, lejos está de ser una intuición mágica o un insight de especialistas.
** Para la realización de las estrategias en la resolución de ejercicios puede verse Mates (1979, pp. 161 y ss.) y Falguera Lopez y Martínez Vidal (1999, pp. 265-310).

2. Dado el siguiente razonamiento, establezca cómo se deriva su conclusión a partir de las reglas de deducción natural de Gentzen:

Db → (Fb ∧¬Rb), Ab →¬Rb, Rb Ⱶ ¬ (Db ∨ Ab)

Segunda parte

Presentación de las reglas para cuantificadores

Reglas para el cuantificador universal

Restricciones: la fórmula de la que se derivará ∀xΦ tiene que contener una constante arbitraria. Por lo tanto: (i) la constante a no debe ocurrir en ningún supuesto (sea premisas o auxiliar) previo no cancelado. (ii) La constante de individuo a no debe ocurrir en la conclusión o en la matriz del generalizador (Φ).

Reglas para el cuantificador existencial

Restricciones: la fórmula de la que se derivará χ tiene que contener una constante arbitraria. Dado que ∃xΦ significa que alguna constante satisface Φ pero no sabemos cuál es. Por lo tanto: (i) la constante a no debe ocurrir en ningún supuesto (sea premisas o auxiliar) previo no cancelado de la derivación. (ii) La constante de individuo a no debe ocurrir en la conclusión o en la matriz del existencial (Φ). (iii) La constante a no debe aparecer en χ.

Justificación intuitiva de las reglas de I∀ y E∃

La siguiente justificación tiene como objeto proporcionar particularmente un esclarecimiento sobre la forma en la que operan las dos reglas con restricciones. Entendemos que no desarrollan ninguna dificultad a la comprensión intuitiva de los estudiantes el modo en que operan las reglas de E∀ y I∃, por lo que la explicación de las mismas no merece mayor detenimiento. Dicho esto, entonces las siguientes justificaciones de I∀ y E∃ se tratan de un complemento didáctico que se le agrega al enfoque sintáctico de la consecuencia. Ahora bien, no podemos dejar de apuntar que, para algunos docentes, la sola presentación de las reglas del sistema podría ser entendida como suficiente para mostrar el enfoque sintáctico de la inferencia.^[6] A nuestro juicio, las reglas se pueden incorporar mejor si se integran de modos confluyentes, toda vez que se pueda, las dimensiones semánticas y sintácticas. Por tanto, estas justificaciones están hechas para predicados monádicos aunque son extensibles a predicados poliádicos en el caso de anidamiento de cuantificadores. El hecho de que la justificación sea intuitiva, demanda que nos apoyemos en consideraciones semánticas aunque, debemos dejar en claro una vez más, que este tipo de consideraciones son ajenas al momento en que se presentan las reglas en sentido estricto. Ahora bien, esa vinculación que realizamos en el terreno didáctico porque la vemos necesaria, también se encuentra en el ámbito teórico de la lógica: “si bien en la presentación original de muchas lógicas se sigue el enfoque semántico y en otras el enfoque sintáctico, hay una suerte de acuerdo tácito que considera que la tarea del lógico no se encuentra concluida hasta que para una misma lógica no se haya conseguido una presentación coincidente desde ambos enfoques” (Alchourrón, 1995, p. 22; Cf., Palau, 2002, sección 2.2)

La regla de I∀

Las restricciones que presenta la regla avalan que se elegirá a una constante que representa, denotan, a un individuo cualquiera del dominio. En este sentido hablamos de constantes arbitrarias (GAMUT, 2002, p. 151), constantes críticas (Falguera López y Martínez, 1999, p. 269) o parámetro propio de la deducción (Legris, 2001, cap. 5). Asimismo se comportan como cuasi variables o seudo constantes, por lo que no pueden aparecer en la conclusión de la derivación (Ibid). Por lo tanto, ∀xPx se sigue de sustituir todas las ocurrencias de una constante de individuo en P, por la ocurrencia de la variable x.

La regla pretende que a cada uno de los términos de individuo del universo del discurso (constantes de individuo: a, b, c, d, etc.) les “quepa” la propiedad P. No sería correcta la aplicación de esta regla si se sustituyeran una parte de las ocurrencias de constantes de individuo por la variable x, y otras no (Falguera López y Martínez, 1999, p. 271).

Dos ejemplos de esta aplicación incorrecta serían:

Esta regla puede ser entendida reflejando la correcta generalización “si vale para cada uno (tomado individualmente), entonces vale para todos” (Legris, 2001, c. 4).

En este sentido ∀x ∃x es verdadera si y sólo si también lo es la conjunción de

Φ[a/x]∧Φ[b/x]…∧Φ[n/x]

La regla podría pensarse como Φa ∧ Φb… ∧ Φn / ∀xΦx

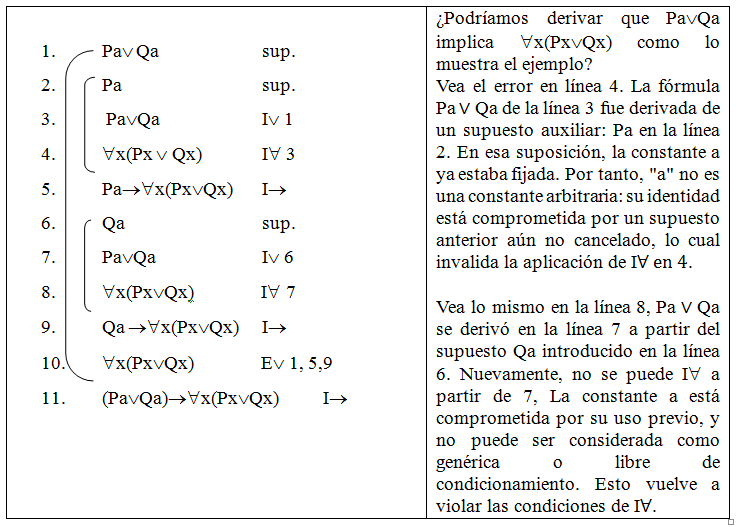
Un ejemplo representativo que permite ilustrar el funcionamiento práctico de una regla como la introducción del cuantificador universal (I∀) puede formularse del siguiente modo. Supongamos que se desea averiguar si el Lote φ de aspirinas ha sido producido de acuerdo con los protocolos exigidos y, por lo tanto, si cada una de las aspirinas contenidas en él es eficaz para aliviar dolores de cabeza. Frente a este objetivo, pueden concebirse dos estrategias lógicas distintas.

1. Por un lado, si se opera conforme a la regla (I∀), basta con seleccionar una constante individual arbitraria —por ejemplo, una aspirina cualquiera del lote— y demostrar que dicha unidad cumple la propiedad correspondiente (alivia dolores de cabeza), siempre que esa constante no posea ninguna particularidad que la distinga del resto del dominio. En este caso, si se logra establecer la propiedad para un ejemplar genérico, y si no se ha hecho ningún supuesto particular sobre él, se puede concluir válidamente que todas las aspirinas del lote poseen dicha propiedad.
2. Por otro lado, si se recurriera a una estrategia más rudimentaria —análoga a una conjunción extensa del tipo φ[a/x] ∧ φ[b/x] ∧ … ∧ φ[n/x]—, entonces sería necesario verificar de manera individual cada elemento del dominio. Es decir, se requeriría examinar una por una todas las aspirinas del lote para asegurar que cada una satisface la propiedad en cuestión. Esta operación, aunque conceptualmente posible, se torna rápidamente inviable si el dominio es muy grande o infinito. El número de pasos requeridos para construir una conjunción finita depende directamente de la cardinalidad del dominio, lo que hace que esta estrategia pierda toda eficacia práctica cuando se trata de conjuntos amplios o ilimitados. Este contraste, véase ilustrativamente que si se hierven tres papas similares para preparar un puré, puede ser razonable probar cada una de ellas para determinar si están en su punto. Sin embargo, si se tratara de verificar la cocción de cien papas, o de una cantidad indefinida, resultaría mucho más adecuado —en términos lógicos y prácticos— seleccionar una muestra arbitraria y representativa, y razonar sobre ella bajo el principio de generalidad. Esto es precisamente lo que permite la regla I∀: afirmar una universalidad a partir de un caso individual no distinguido, bajo condiciones normativas bien definidas.

En suma, este ejemplo evidencia que la lógica formal no es sólo un ejercicio abstracto, sino que puede modelar decisiones racionales cotidianas y científicas. La pertinencia de una regla como I∀ está directamente asociada a la necesidad de operar sobre dominios extensos de manera eficiente, sin comprometer la validez del razonamiento.

Más allá de la cardinalidad del dominio considerado y de la inviabilidad práctica de recorrerlo exhaustivamente, lo fundamental en el funcionamiento de la regla (I∀) no radica en la cantidad de elementos sino en las restricciones estructurales que garantizan la corrección inferencial. La clave reside en el uso de una constante arbitraria, es decir, una constante que no representa ningún individuo particular del dominio, sino que actúa como representante genérico del mismo. Por eso, para que esta constante pueda ser legítimamente generalizada mediante I∀, debe cumplir las restricciones que no son condiciones meramente formales, sino que cumplen una función epistemológica y semántica esencial: impiden que se derive una generalización universal a partir de un caso especial, accidental o ad hoc. De este modo, la identidad de la constante arbitraria debe permanecer irreconocible dentro del desarrollo deductivo. No se trata, pues, de que el valor de esa constante sea desconocido en sentido empírico, sino de que su estatuto lógico no debe estar comprometido por ninguna dependencia externa. Su aislamiento respecto del resto de la derivación es lo que habilita la validez del paso inferencial desde un caso genérico al enunciado universal.

La regla de E∃

Esta regla puede comenzar a explicarse mediante el siguiente ejemplo práctico. Si yo dijera que hay un alumno del curso que aprobó el primer parcial y, además, que ningún alumno que aprueba ese parcial está triste, de eso puede concluirse que habrá un alumno que no esté triste.

Este ejemplo sugiere una idea clave: no es necesario conocer la identidad del individuo que satisface la fórmula existencial para derivar válidamente una conclusión. Lo que se requiere es suponer que existe al menos uno, con la condición de que dicha suposición se realice conforme a las restricciones técnicas que establece la lógica formal.

En términos precisos, la regla de E∃ permite, a partir de una fórmula ∃x φ(x), suponer que existe un individuo —representado por una constante arbitraria “a”— que satisface φ(a). Sin embargo, esa constante no puede ser ninguna constante concreta ya presente en las premisas, en la conclusión ni en ningún supuesto auxiliar no cancelado. Se trata, como en el caso de (I∀), de una constante que actúa como representante de una entidad cualquiera del dominio, sin que se le atribuya ninguna identidad específica.

Por ello, sería lógicamente incorrecto inferir de ∃x Px que Pa, si “a” ya aparece en la derivación o si se trata de un individuo determinado del dominio. Lo que permite la validez de la inferencia es justamente la arbitrariedad de la constante y el hecho de que esta aparezca únicamente en un supuesto auxiliar abierto para la aplicación de E∃.

En la estructura del ejemplo, la fórmula ψ debe ser independiente de la constante arbitraria introducida. Esto significa que ψ podría haber sido obtenida a partir de φ(b), φ(c), etc., mientras se cumplan las condiciones mencionadas. Esta independencia garantiza que no se extraiga información indebida del uso de una instancia existencial particular.

Seguramente, como este ejemplo lo sugiere, no precisaría de conocer la identidad precisa de quién aprobó para poder derivar esa conclusión de las premisas dadas. En sentido estricto, al menos una entidad concreta del dominio, si sustituyera a la variable de individuo, permitirá que derive la fórmula que tengo como conclusión. De la E∃ de la fórmula ∃xPx se seguiría una inferencia incorrecta si aseveramos que una constante de individuo concreta y determinada del dominio le pertenece el atributo que representamos como P. Las restricciones que operan en la regla no permiten este tipo de inferencias, sino que nuevamente se exige que establezcamos (esta vez en calidad de supuesto auxiliar) la existencia de una constante arbitraria que no puede aparecer en premisas, conclusión o supuestos no cancelados. Esta constante, como dijimos, no da cuenta de alguna constante determinada sino que denota una entidad cualquiera del dominio (Falguera López y Martínez, 1999, p. 281). La fórmula que cancela el supuesto auxiliar que se abrió con la constante arbitraria es una fórmula a la que se podría haber derivado también con cualquier otra que cumpliera las condiciones establecidas (i.e., Φ[a/x] ∨Φ[b/x]…∨Φ[n/x]).

Ejercicios: A partir de las reglas del SDN derivar mutuamente las siguientes fórmulas.

El objetivo pedagógico de los ejercicios que siguen es clarificar la inter definición de los cuantificadores. En particular, se proponen pares de fórmulas cuya derivación mutua, mediante reglas del sistema de deducción natural (SDN), permite observar empíricamente cómo se comportan las negaciones de cuantificadores existenciales y universales.

1. ∃xPx ˧Ⱶ ¬∀x¬Px (definición del existencial)
2. ∀xPx ˧Ⱶ ¬∃x¬Px (definición del universal)
3. ¬∀xPx˧Ⱶ ∃x¬Px (negación del universal)
4. ¬∃xPx ˧Ⱶ ∀x¬Px (negación del existencial)

Soluciones, conjuntamente con la presentación de las correspondientes estrategias deductivas

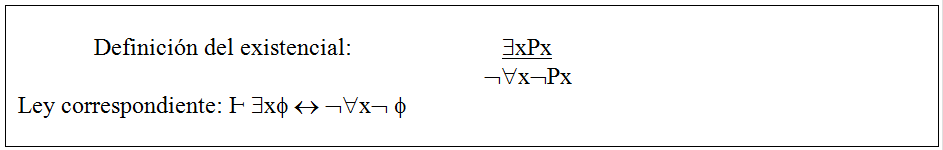
Consideraciones finales

A lo largo de estas notas hemos recorrido algunos de los elementos centrales del sistema de deducción natural en la lógica de predicados de primer orden, con atención tanto a las reglas formales como a las estrategias que orientan su aplicación. El eje que organizó este recorrido no fue exclusivamente técnico: estuvo guiado por la convicción de que enseñar lógica requiere algo más que exponer reglas y ofrecer ejercicios. Supone formar un tipo específico de competencia racional, orientada a la justificación, la explicitación de supuestos y el control normativo del paso de unas proposiciones a otras. En este sentido, el aprendizaje del sistema deductivo debe concebirse como una práctica que articula estructura formal y decisión estratégica, corrección sintáctica y comprensión conceptual.

La deducción no constituye un método de decisión, en el sentido técnico del término, ya que no proporciona un procedimiento finito y efectivo que permita determinar, para toda fórmula dada, si esta puede ser derivada a partir de un conjunto de premisas. Ante una fórmula arbitraria, no siempre es posible saber si existe una derivación válida que la justifique, y si no la encontramos, ello no implica que no exista: dado que el número de posibles derivaciones es infinito, carece de sentido esperar que la no aparición de una derivación en un intento particular permita concluir su inexistencia. No obstante, a pesar de esta limitación, sabemos que LPO es correcta y completa. Esto significa que, para todo conjunto de fórmulas φ₁… φ_n╞ ψ si y sólo si φ₁… φ_n ├ ψ: es decir, ψ es consecuencia lógica (en sentido semántico) de φ_₁… φ_n si y solo si existe una derivación formal (en sentido sintáctico) de ψ a partir de ellas. Esta correspondencia entre validez semántica y deducibilidad sintáctica está establecida por los metateoremas de corrección^[7] y completitud, ^[8] que articulan de manera rigurosa la relación entre los modelos lógicos y los sistemas de prueba.

La enseñanza de la deducción natural obliga a habitar —y no simplemente a resolver— la tensión entre la intuición y el formalismo. Por un lado, es deseable que el estudiante reconozca en una derivación algo que le “hace sentido” que no le resulte ajeno a sus prácticas de razonamiento. Por otro, el sistema exige el cumplimiento estricto de condiciones que muchas veces contrarían nuestras intuiciones más inmediatas. Lejos de suponer un obstáculo, esta tensión constituye el terreno formativo.

En paralelo, es necesario reconocer que el razonamiento humano no se agota en su dimensión normativa. Los trabajos de la psicología del razonamiento han mostrado de modo sistemático que los seres humanos no razonan siempre conforme a las reglas que los lógicos consideran válidas, y que nuestros procesos inferenciales se ven condicionados por factores como la economía cognitiva, el contexto, la familiaridad o los sesgos adquiridos. Esta constatación no invalida la lógica formal; por el contrario, le da una función aún más relevante: no la de describir cómo razonamos, sino la de establecer estándares públicos y justificables sobre cómo deberíamos razonar en contextos donde la validez y la transparencia importan.

Por todo esto, la enseñanza de la deducción natural debe aspirar a formar agentes capaces de evaluar críticamente los movimientos inferenciales que realizan, no operadores automáticos. Se trata de ofrecer al estudiante herramientas para construir, reconstruir y revisar razones.

Referencias bibliográficas

Alchourrón, C. (1995). “Concepciones de la lógica”. En Enciclopedia Iberoamericana de Filosofía. Lógica (pp. 11–48). Madrid: Trotta.

Alonso, E. (2011). Cálculo; Decidibilidad. En L. Vega Reñón & P. Olmos Gómez (Eds.), Compendio de lógica, argumentación y retórica (pp. 89–90; 168–169). Madrid: Editorial Trotta.

Busdygan, D. (2023). “Argumentación moral”. EN: G. Lariguet (Dir); G. Lariguet, M.S. Yuan, N. Alles (Comps.). La metaética puesta a punto. Santa Fe: UNL, pp. 199-213.

Corcoran, J. (2011). “Deducción / Deducibilidad”. En L. Vega Reñón & P. Olmos Gómez (Eds.), Compendio de lógica, argumentación y retórica (pp. 168–170). Madrid: Editorial Trotta.

Daguerre, M. y Elgarte, J. (2018). La normatividad en ética y en lógica: una perspectiva evolutiva (Proyecto de investigación PI+D H852). Universidad Nacional de La Plata. Facultad de Humanidades y Ciencias de la Educación. Centro de Investigaciones en Filosofía.

Falguera López, J. L., & Martínez Vidal, C. (1999). Lógica clásica de primer orden. Estrategias de deducción, formalización y evaluación semántica. Madrid: Trotta.

Gamut, L. T. F. (2002). Introducción a la lógica (C. Durán, Trad., 3.ª ed.). Buenos Aires: Eudeba.

Legris, J. (2001). Deducción y representación. Una introducción a la lógica de primer orden. Buenos Aires: Economizarte.

Marraud, H. (2011). “Derivación / Derivabilidad”. En L. Vega Reñón & P. Olmos Gómez (Eds.), Compendio de lógica, argumentación y retórica (pp. 187–190). Madrid: Editorial Trotta.

Mates, B. (1979). Lógica matemática elemental. Madrid: Técnos.

Nisbett, R. E. (2016). Mindware: Herramientas para pensar mejor. Debate.

Palau, G. (2002). Introducción filosófica a las lógicas no clásicas. Barcelona: Gedisa.

Quesada, D. (1995). “Lógica clásica de primer orden”. En Enciclopedia Iberoamericana de Filosofía. Lógica (pp. 71–105). Madrid: Trotta.

---