En este capítulo se comentan las ventajas que señalan quienes pertenecen al neomecanicismo como propias de la búsqueda, identificación, modelación de mecanismos y explicación mecanicista. Como ya se ha señalado, la investigación científica neomecanicista surge en distintas disciplinas o ámbitos y, hasta el momento, no ha sido tratada de manera general, como un movimiento dentro de “la” ciencia (a secas). Es por esto que, a la hora de poner los mecanismos en un rol central, las ventajas señaladas son, en general, presentadas para ciertas disciplinas específicas (con algún comentario marginal, a lo sumo, sobre la utilidad en otras áreas).

En la literatura neomecanicista suelen señalarse cuatro ámbitos en los cuales los mecanismos resultan provechosos para la ciencia y/o la filosofía: en la explicación de fenómenos, en el acceso a la interdisciplinariedad, en el tratamiento de la causalidad y en la investigación. A estos temas se los tratará in extenso en los primeros cuatro parágrafos de este capítulo, ya que no son particulares de una disciplina o área, sino que por su alcance pueden verse como propios del enfoque neomecanicista. El problema de la causalidad^[1] es un problema más bien filosófico, o, en todo caso, un problema metafísico que atañe a la ciencia. La preocupación científica es reconocer las distintas causas, lo cual no significa que la ciencia deje de lado el problema de la causalidad (en general), sino que no es un problema propio de una disciplina científica particular y, como tal, pueda ser abordado desde el seno de una disciplina. Los otros tres puntos en que los mecanismos resultan provechosos son más bien de índole científica y, si bien son presentados desde alguna disciplina particular, podrán servir a otras disciplinas.

En el último parágrafo de este capítulo se comentan brevemente algunas ventajas más, aunque no se las trata en detalle porque son, más bien, “locales”, ya que solamente ciertas disciplinas podrán aprovecharlas. Son, de todas maneras, ventajas del enfoque.

Este capítulo aporta algo novedoso: un análisis sistemático y detallado de los beneficios que brinda la investigación neomecanicista (es decir, un análisis que abarca todas las disciplinas). Este tipo de análisis no se ha hecho hasta el momento y resultará útil para complementar la presentación y propuesta del enfoque neomecanicista. Dado que muestra el atractivo que el enfoque tiene para las distintas disciplinas científicas y la filosofía, el análisis puede resultar útil para sumar nuevos neomecanicistas y consolidar la propuesta.

1. Explicación y comprensión

Una de las tareas de la ciencia es explicar. Explicar es responder a la pregunta “¿por qué?”, y una buena explicación debe dar la respuesta de manera tal que se comprenda por qué pasó (o pasa) lo que se quiere explicar. Uno de los principales argumentos de los autores neomecanicistas consiste en mostrar que la explicación mecanicista es una buena estrategia explicativa, per se y frente a otros modelos de explicación. Este argumento está presente en toda la literatura neomecanicista, independientemente de qué disciplina se trate (y, como se dijo en el final del capítulo 2, una estrategia común entre neomecanicistas consiste en mostrar que dar explicaciones mecanicistas es tarea habitual en sus disciplinas). Para resaltar las virtudes de la explicación mecanicista, usualmente se la presenta en contraposición con algún otro tipo de explicación o modelo explicativo conocido. La estrategia usual, que es la que se empleará aquí, consiste en exponer en primer término el modelo de explicación científica estándar y mostrar algunas de sus limitaciones, ya sea en cuanto a su poder explicativo, ya sea respecto de su aplicación. Las críticas y objeciones al modelo estándar revelarán la necesidad de buscar, en ciertas disciplinas al menos, modelos explicativos alternativos. En segundo lugar, se caracterizará en detalle el modelo de explicación mecanicista y se mostrará cómo suple las deficiencias del modelo estándar y cómo puede aventajarlo en cuanto a la comprensión que brinda del fenómeno a explicar. Finalmente, se expondrán otras estrategias de explicación científica propuestas como alternativas a la explicación estándar^[2] y se mostrará que la explicación mecanicista se presenta como más ventajosa que ellas. Es menester aclarar que los modelos explicativos que aquí se discuten no son todos los existentes, por lo cual no se muestra que la explicación mecanicista sea la mejor. Se muestra que en ciertas disciplinas los modelos más difundidos no resultan satisfactorios (al menos, para explicar algún tipo de fenómeno) y la explicación mecanicista constituye una buena alternativa. En las disciplinas en las que se disponga de modelos explicativos adecuados, la explicación mecanicista podrá ser vista como un modelo complementario.

1.1. La explicación nomológico deductiva

El modelo de explicación científica más difundido y discutido, y al que aquí se ha llamado “estándar”, es el modelo propuesto por Hempel y Oppenheim (1948)^[3] –y desarrollado por Hempel (1962, 1965, 1966)–: el modelo nomológico deductivo^[4]. La estrategia explicativa es la siguiente: explicar un fenómeno consiste en subsumirlo a leyes. Es decir, consiste en mostrar que el fenómeno que se pretende explicar (descripto en el enunciado explanandum) es perfectamente esperable, dadas las leyes que rigen los fenómenos. Los enunciados que explican conforman el explanans. En este modelo, el explanans y el explanandum toman la forma de un razonamiento en el cual el explanandum es la conclusión.

Por ejemplo, supóngase que se pretende explicar por qué una botella que contenía agua y que estuvo toda la noche en el congelador se rompió. Informalmente, la explicación, según el modelo nomológico deductivo, sería algo así: “el agua en el congelador se solidifica; cuando se congela, el agua se expande; la presión que ejerce al expandirse el agua partió el vidrio”. Usualmente, una explicación de este tipo resulta suficiente, dado que quien recibe la explicación recupera lo que en ella está implícito, por ejemplo, que el congelador mantiene una temperatura relativamente constante inferior a 0º C y que el vidrio no es elástico y su resistencia es inferior a la presión que ejerce el agua. Si se quiere explicitar un poco más la explicación, podrá decirse: “la botella de vidrio estaba llena de agua corriente. El congelador mantiene la temperatura debajo de 0º C, por lo cual la botella –y el agua contenida en ella– estuvo a una temperatura inferior a 0º. El agua corriente se solidifica por debajo de los 0º C. Al solidificarse, el agua se expande. El agua de la botella no tuvo lugar suficiente para expandirse al congelarse. La presión que ejerce el agua al solidificarse es mayor que la resistencia que opone el vidrio. Dado que el vidrio no es elástico, cuando se ve sometido a una presión superior a la que resiste, se parte”. De lo anterior se sigue que la botella se partió.

Del ejemplo puede abstraerse la forma general que toma este tipo de explicación. Por una parte hay leyes (L1, L2, etc.), y por otra, se tienen descripciones de las condiciones que rodearon el fenómeno a explicar. A estas descripciones se las denomina “condiciones iniciales”^[5] (C1, C2, etc.). De las leyes y las condiciones iniciales se deduce lógicamente el explanandum. Esquemáticamente, la explicación del ejemplo sería:

(L1) El agua corriente se solidifica por debajo de 0º C.

(L2) El agua se expande cuando se solidifica.

(L3) El vidrio no es elástico y se parte cuando se ve sometido a una presión superior a la que resiste.

(L4) La presión que ejerce el agua al expandirse en el proceso de solidificación es superior a la presión que resiste el vidrio.

(C1) La botella de vidrio estaba llena de agua corriente.

(C2) La botella estuvo toda la noche en el congelador.

(C3) El congelador mantiene la temperatura por debajo de 0º C.

(Explanandum) La botella se rompió.

En el ejemplo, lo que se quiere explicar es un hecho particular, lo que le pasó a una determinada botella. Pero el explanandum puede describir un fenómeno general, por ejemplo, que las botellas de vidrio llenas de agua se rompen cuando pasan la noche en el congelador. En este caso, el explanans deberá contener las leyes, pero las condiciones iniciales no aparecerán, ya que, como se dijo, las condiciones iniciales son las que rodean al fenómeno particular (que esta botella de agua estuvo en este congelador; que este congelador mantuvo la temperatura bajo cero; etc.).

La explicación nomológico deductiva debe su nombre a que el explanans contiene leyes (nomos es ley en griego) y a que el explanandum se deduce lógicamente del explanans. Es un razonamiento que contiene al menos una ley entre sus premisas. Pero no todo razonamiento que contiene al menos una ley entre sus premisas es una explicación nomológico deductiva; para serlo, debe cumplir los siguientes requisitos:

R1. El explanandum debe ser una consecuencia lógica del explanans.

R2. El explanans contiene enunciados solamente de manera esencial (es decir, si se quitara del explanans uno solo de esos enunciados, el explanandum ya no podría derivarse lógicamente).

R3. El explanans debe contener al menos una ley^[6].

R4. Los enunciados explanantes (los que conforman el explanans) deben tener alcance empírico (es decir, deben describir fenómenos susceptibles de contrastación directa o indirecta).

R5. Si el explanandum describe un hecho particular, el explanans deberá contener al menos una condición inicial. Si el explanandum no describe un hecho particular, el explanans no debe contener condiciones iniciales. (Este requisito se deriva de R1 y R2.)

R6. El explanandum no debe figurar ni explícita ni implícitamente en el explanans.

R7^[7]. Los enunciados explanantes (las leyes y condiciones iniciales contenidas en el explanans) deben ser verdaderos.

El requisito R7 es demasiado fuerte. Es razonable poner como requisito que las condiciones iniciales estén verificadas (es decir, que la evidencia pruebe que efectivamente ocurrió lo que describen), pero los enunciados universales, como las leyes que pretende el modelo, no pueden ser verificadas, ya que los fenómenos que abarcan las leyes escapan a la experiencia directa. Las leyes pueden, en el mejor de los casos, estar corroboradas (o, lo que es lo mismo, confirmadas, es decir, no estar refutadas por evidencia directa, y estar apoyadas indirectamente, esto es, pertenecer a alguna teoría a la que la evidencia directa ha apoyado y no ha refutado). Este requisito puede entonces reformularse de la siguiente manera:

R7’. Las leyes contenidas en el explanans deben estar corroboradas, y las condiciones iniciales deben estar verificadas.

Si el modelo exige el requisito R7, se tiene el modelo nomológico deductivo. Si el modelo exige el requisito R7’, se tiene el modelo hipotético deductivo de explicación científica (hipotético, porque los enunciados generales son hipótesis no refutadas). Esta distinción no está presente en todos los textos que exponen el modelo estándar, y no será relevante para lo que sigue. De la definición de verdadero y de corroborado se sigue que el requisito R4 está implicado por R7 y por R7’.

No cabe duda alguna de que este modelo explicativo es de gran atractivo, y aquí se lo ha llamado “estándar” justamente porque es el modelo explicativo que figura en todos los manuales de filosofía de la ciencia de las últimas 5 décadas (aunque más no sea, para discutir su pretensión de erigirse en el modelo de explicación científica). Una de las razones de este atractivo es la llamada simetría entre la explicación y la predicción, que sostiene que la única diferencia entre explicación (de un hecho particular) y predicción es pragmática: en la explicación, el explanandum describe un hecho que ya ha ocurrido (es decir, el explanandum está debidamente verificado); en la predicción, el explanandum describe un hecho que todavía no ha ocurrido. Por lo demás, la estructura de una predicción (y esto diferencia la predicción científica de la profecía) es idéntica a la de una explicación nomológico deductiva, incluidos los requisitos R1–R7 (o R7’). La tesis de la simetría entre explicación y predicción “equivale a la conjunción de dos subtesis, a saber: 1) que toda explicación adecuada es potencialmente una predicción, en el sentido ya indicado; 2) que, a la inversa, toda predicción adecuada es potencialmente una explicación”^[8] (Hempel, 1979, p. 362)^[9]. Y la predicción juega un rol central en la evaluación de los enunciados que componen una teoría^[10] y en las llamadas “experiencias cruciales” que permiten decidir entre teorías o hipótesis distintas que pretenden explicar el mismo fenómeno. Pero a pesar del atractivo, este modelo explicativo presenta algunos inconvenientes. Las críticas que se han hecho a este modelo explicativo son diversas, y pueden dividirse en dos grupos: críticas al modelo y problemas de aplicación del modelo explicativo.

Para presentar las críticas al modelo nomológico deductivo, puede comenzarse señalando que el modelo nomológico deductivo se caracteriza por dos supuestos: (1) el modo primario de representar las explicaciones es proposicional, y (2) la lógica provee las herramientas para razonar sobre esas representaciones (Bechtel y Abrahamsen, 2005, p. 427).

Con respecto a (1), puede señalarse que en biología, geología, química, y otras ciencias, una de las características salientes de casi cualquier trabajo es su dependencia de representaciones espacio-visual, como fotos, grafos o esquemas. Los diagramas, en particular, pueden jugar un papel central al presentar una explicación. El modelo nomológico deductivo privilegia la forma proposicional o lingüística a punto tal que las imágenes y, gráficos solo pueden cumplir un rol esencialmente secundario: la inferencia lógica es una relación entre enunciados, no entre hechos, fotos o mapas.

Con respecto a (2), uno de los problemas propios de la lógica deductiva es el grado de comprensión que brinda^[11]. Explicar es siempre, como se dijo, responder a la pregunta “¿por qué?”. Una respuesta satisfactoria debe ser final, es decir, debe brindar una comprensión completa y no generar nuevos “¿por qué?” Como señala Bunge (1997), si se pregunta “¿por qué murió Sócrates?”, resulta insatisfactoria la explicación que reza: “todos los seres humanos son mortales y Sócrates es un ser humano”. Esta explicación nomológico deductiva no brinda ninguna comprensión sobre el porqué de la muerte de Sócrates.

El otro punto criticable del modelo de explicación nomológico deductivo es que requiere leyes, lo cual lo torna inutilizable en todo ámbito científico que carezca de ellas. Si bien es un problema en sí mismo la definición de ley científica^[12], en ciertas disciplinas (en las ciencias sociales, en las llamadas “ciencias de la vida” y en las ciencias conductuales) es altamente discutible la existencia de leyes^[13]. Y no se trata únicamente del requisito R7 sobre la posesión de leyes verificadas, sino también del requisito débil R7’, que requiere leyes corroboradas o confirmadas. El problema que enfrentan las disciplinas sin leyes entonces es: o bien deben limitarse a describir (responder a la pregunta “¿qué?” sin poder responder a la pregunta “¿por qué?”) o bien deben buscar una estrategia explicativa diferente, que no requiera leyes. Por esto, para no renunciar a la tarea explicativa, se han propuesto modelos explicativos alternativos^[14], como los que se expondrán a continuación. Para quienes sostienen que se dispone de leyes confirmadas en las distintas disciplinas^[15], esta crítica al modelo nomológico deductivo no sería tal. Queda, de todas maneras, la objeción respecto del poco contenido explicativo de las leyes y del modelo.

1.2. El modelo de explicación mecanicista^[16]

Como se dijo, un mecanismo opera en la realidad; un modelo mecanicista es un constructo analítico que emula un mecanismo; una explicación mecanicista es una actividad epistémica que utiliza un modelo mecanicista para explicar un fenómeno. El corazón de María es un sistema con dos mecanismos. El modelo del bombeo del corazón dado en el capítulo 2 es una caracterización que pretende capturar las características esenciales de los mecanismos que hacen circular la sangre. Explicar por qué circula la sangre (o por qué circula la sangre de María) es utilizar ese modelo (o uno similar). El modelo puede ser (al igual que la explicación) más o menos general: así como puede explicarse por qué circula la sangre de María o por qué circula la sangre de los mamíferos, de la misma manera puede modelarse el mecanismo de sístole (propio del corazón) o el mecanismo de bombeo (que simplemente muestra la dinámica de un fluido ante la compresión del recipiente contenedor). La relación entre el modelo y el mecanismo es de emulación, y esta solamente es posible hasta cierto punto, es decir, el modelo captura ciertos detalles del mecanismo. El principal requisito para que el modelo realmente permita explicar el fenómeno que el mecanismo causa es de adecuación: las unidades, propiedades, relaciones y demás elementos del modelo deben encontrarse en el mecanismo. No necesariamente deben “verse”, ya que, como se dijo, algunas unidades pueden no ser observables. Pero sí debe tenerse evidencia, aunque sea indirecta, de la presencia de esas unidades, de las propiedades y relaciones de esas unidades, etc. En términos de Craver (2006, p. 361), pueden proponerse distintos modelos para un mismo mecanismo; un modelo que no cumple con el requisito de adecuación solamente es un modelo how possible, una explicación mecanicista requiere un modelo how actually, es decir, un modelo cuya adecuación esté confirmada.

Los modelos mecanicistas pueden ser lingüísticos o diagramáticos, utilizar imágenes, gráficos, mapas, animaciones y otros recursos. Para representar las distintas relaciones entre las unidades se puede apelar a cualquier recurso: a gráficos, esquemas, fotos y mapas para las relaciones espaciales; a flechas, líneas y animaciones para las relaciones temporales; a gráficos y ecuaciones matemáticas para las resultantes de las relaciones. Las regularidades podrán representarse lingüística o proposicionalmente (particularmente, si se tiene leyes, ya sean deterministas o estadísticas), con gráficos de distribución de frecuencias, con modelos computacionales, formulaciones matemáticas (como los juegos), entre otras. Aunque la modelación de mecanismos siempre puede apelar a la formulación lingüística, no está limitada a ella. Lo relevante es siempre mostrar el modus operandi, el patrón de acción característico que permite establecer las sucesivas etapas. La estrategia explicativa consiste en describir el mecanismo, lo cual muestra cómo se produjo el fenómeno^[17]. Este punto de la flexibilidad representacional es esencial o distintivo, ya que las demás estrategias explicativas se ven limitadas a la formulación lingüística (o, en todo caso, toman la formulación lingüística como privilegiada).

La principal ventaja de usar diagramas es obvia: a diferencia de las representaciones lingüísticas o proposicionales, los diagramas usan el espacio para transmitir información. La distribución y organización espacial son usualmente claves para la operación de un mecanismo, y pueden ser fácilmente mostradas en un diagrama. Incluso cuando la organización espacial no sea relevante, los diagramas pueden ser usados para relacionar o separar conceptualmente las unidades, operaciones, actividades o relaciones relevantes.

También la relación temporal es importante en los mecanismos: dos mecanismos pueden ser concatenados, simultáneos o sucesivos. Esto puede ser capturado en los diagramas, usando las dimensiones espaciales para transmitir el orden temporal. Para ello, suelen usarse flechas o representaciones en tres dimensiones. Esta ventaja inmediata que toman los diagramas sobre las representaciones lingüísticas, la de presentar a la inspección simultáneamente tanto las partes como las operaciones, es la menor de todas. Después de todo, la gente tal vez mire (o pueda mirar) solo una parte del diagrama. Una ventaja mayor es que los diagramas ofrecen recursos para una representación relativamente directa, icónica.

Como se dijo, los mecanismos representados mediante diagramas también pueden ser descriptos lingüísticamente. Cabe preguntarse si existe alguna diferencia fundamental entre la representación lingüística y la diagramática. Para Larkin y Simon (1987) los diagramas y las representaciones lingüísticas son informacionalmente equivalentes pero difieren en dos aspectos importantes: en primer lugar, la búsqueda y el reconocimiento de patrones en la representación diagramática es más fácil; en segundo lugar, las representaciones difieren en cuanto a los procedimientos de inferencia que pueden aplicársele a los patrones que se reconocen. En parte, esas diferencias tienen su origen en que la información que puede estar solo implícita en una representación lingüística puede estar explícita, y de hecho, de manera más sencilla que en un razonamiento, en un diagrama. Larkin y Simon (1987, p. 65) sostienen que, dada la disposición espacial de la información, la resolución de problemas puede proceder mediante un recorrido lento a través del diagrama, y puede requerir muy poca búsqueda o cómputo de los elementos implícitos. Stenning y Lemon (2001) sugieren otra ventaja: que los diagramas son más limitados en poder expresivo que las proposiciones y, consecuentemente, más tratables.

Si los diagramas son un vehículo importante para representar mecanismos, será necesario considerar cómo se razona sobre diagramas. En particular, si los diagramas brindan información que no es dada (o fácilmente presentada) en representaciones lingüísticas, entonces la inferencia lógica (que relaciona el explanans con el explanandum en el modelo nomológico deductivo y en otros modelos de explicación) no capturará el razonamiento involucrado en la comprensión sobre cómo un mecanismo dado produce el fenómeno que se quiere explicar. La clase de razonamiento necesaria para comprender los diagramas es la clase de razonamiento que captura la operación del mecanismo, incluyendo las relaciones entre unidades, las operaciones que ejecutan y la manera en que esas operaciones se relacionan unas con otras.

Una limitación del diagrama es su condición de estático, aunque los diagramas animados pueden salvar esta dificultad. Es el agente cognitivo el que debe imaginar las diferentes operaciones que se ejecutan, trocando así una representación estática en algo dinámico. Mary Hegarty, en un artículo que estudia el llamado “razonamiento mecánico”^[18], sugiere (Hegarty, 1992, p. 1084) el término animación mental (mental animation) para la actividad de inferir el estado de un componente del sistema dada la información sobre los estados de, y las relaciones entre, los otros componentes del sistema. En un experimento, donde se tomaban datos sobre el tiempo de reacción y el movimiento ocular mientras los sujetos resolvían problemas (sobre mecanismos relativamente simples de poleas), Hegarty encontró que a los sujetos les resultaba más simple hacer inferencias que requerían razonar sobre estados futuros del sistema que sobre estados pasados; esto sugiere que los sujetos animaban el sistema secuencialmente a partir de lo que se representaban como la primera operación. Además, Hegarty (que investiga hasta qué punto los procesos de inferencia son isomórficos con la operación de los sistemas físicos), nota que los sujetos hacen inferencias separada y secuencialmente sobre diferentes componentes del sistema, incluso si en el sistema físico los componentes operan simultáneamente (con lo cual, los procesos de inferencia no son isomórficos a la operación de los sistemas físicos). Es decir, el tipo de razonamiento involucrado en la comprensión de un esquema es la animación mental que, si bien no es un proceso isomórfico a la operación de los mecanismos físicos, permite “animar” las diferentes unidades o componentes y la comprensión de la conducta del mecanismo (con mayor facilidad, la representación de la operación en estados futuros).

Una pregunta que surge inmediatamente es cómo las personas animan los diagramas de mecanismos para entenderlos. Una posible respuesta es que crean y transforman una imagen del mecanismo para representarse los diferentes componentes y el modo en que cada uno lleva a cabo sus operaciones. La investigación en neurociencia cognitiva de Kosslyn (1994) indica que cuando se forma una imagen se utilizan muchos de los recursos neuronales que se emplean en la percepción. Como aclaran Bechtel y Abrahamsen (2005, p. 431, nota 13) está lejos de ser plenamente aceptado en ciencia cognitiva que las representaciones formadas en el sistema cognitivo sean realmente similares a las imágenes (Pylyshyn, 1981, 2003; Kosslyn, 1981, 1994). De todas maneras –señalan– lo importante es cómo el sistema cognitivo representa algo, y no la manera en que codifica sus representaciones. Entonces, lo que ocurre en el cerebro al formarse una imagen es una actividad comparable a lo que ocurre al ver, de hecho, una imagen. Barsalou (1999) se refiere a esta actividad neuronal como un símbolo perceptual (perceptual symbol). Pensar con símbolos perceptuales implica que el cerebro inicia secuencias de operaciones que se corresponden con lo que el cerebro habría experimentado si hubiese visto, de hecho, una imagen. Entonces, este imaginar no involucra objetos mentales, solo la actividad de representarse objetos y cómo ellos cambian.

En sistemas muy complejos, que involucran gran cantidad de componentes y operaciones, es común extraviarse. La utilidad de la representación mental alcanza entonces su límite. Los científicos necesitan ir más allá, y para eso existen distintas herramientas que pueden diseñarse para ayudar, como los modelos a escala o simplificados y los modelos matemáticos. La representación y la inferencia en la explicación mecanicista son, entonces, diferentes de la representación y la inferencia en la explicación nomológico deductiva. Aunque es posible dar una descripción lingüística de un mecanismo, esa descripción no es la privilegiada: usualmente la representación preferida para un mecanismo la proveen los diagramas. La inferencia involucra la determinación de la conducta de un mecanismo, y esto típicamente no se obtiene mediante la inferencia lógica, sino mediante la simulación (mediante un diagrama animado, una simulación mental, computacional o un modelo a escala) de la actividad del mecanismo.

Las explicaciones mecanicistas son, además, finales, es decir, no requieren ulteriores explicaciones. Tal vez sea en ciencias sociales donde las explicaciones finales parezcan más difíciles de obtener, debido a la cantidad de elementos que intervienen en los fenómenos de acción colectiva. Baldassarri (2005)^[19] señala algunas de las dificultades que deben sortear las explicaciones de fenómenos de acción colectiva, y sostiene que el modelo explicativo propuesto para las ciencias sociales deberá poder contemplar tres aspectos:

(a) Normalidad/anormalidad: la acción colectiva tiene períodos que pueden considerarse de normalidad o acción colectiva ordinaria (es decir, el funcionamiento de la sociedad en períodos sociales de bonanza, prosperidad o estancamiento) y breves períodos de acción extraordinaria (períodos revolucionarios o catastróficos).

(b) Múltiples niveles: se requieren explicaciones que involucren diferentes niveles de organización; particularmente los individuos, las relaciones entre individuos, y las estructuras que resultan de la interacción entre individuos.

(c) Dinámica histórica: han de poder explicarse fenómenos de acción colectiva que ocurren no solo en el corto plazo, sino también en largos períodos históricos.

El modelo mecanicista de explicación no tiene ningún inconveniente, en principio, para capturar estos tres aspectos. El punto (c) no es problemático: los mecanismos (piénsese, por ejemplo, en los mecanismos de biología evolutiva) pueden estar operando durante largos períodos hasta provocar el estado final. Algunos mecanismos, por el contrario, operan rápidamente, esto permite (si se identifican) explicar los períodos de “anormalidad” del inciso (a). Con respecto a los períodos “de normalidad”, el estado de equilibrio estático no puede, según se sostiene aquí, ser causado por un mecanismo, ya que los mecanismos no “previenen el cambio”, sino que causan cambios. Como se vio en el ejemplo del bombeo del corazón, muchas veces, sin embargo, se habla de “estado de equilibrio” refiriéndose a un estado de cambio permanente, dentro de ciertos límites. En los fenómenos de acción social colectiva durante los períodos “de normalidad” pasa algo similar: no son estáticos, sino dinámicos. Los sistemas sociales están continuamente cambiando, y lo que se considera “actividad normal” es un cambio que se da constantemente, aunque dentro de ciertos límites o parámetros. Si se lo entiende así, entonces puede explicarse, apelando a mecanismos, qué aportan los mecanismos para que el sistema social se mantenga estable (la estrategia usual sería explicar cómo los mecanismos se accionan y logran que los niveles o parámetros no se escapen de los niveles aceptables). Con respecto al inciso (b), la explicación mecanicista no solo no tiene inconvenientes en explicar fenómenos que operan en distintos niveles, sino que es especialmente apta para ello: para una buena explicación mecanicista, además de las unidades, sus propiedades y relaciones, también deben identificarse las circunstancias externas relevantes para saber cómo las variaciones afectan la conducta del mecanismo, y muchos de los componentes del mecanismo pueden, a su vez, ser mecanismos. Es por esto que la explicación mecanicista puede ser recursiva (Bechtel y Abrahamsen, 2005). La reducción tradicional^[20] es también recursiva, pero hay una diferencia importante: en ella, el nivel más primitivo debe dar una descripción comprehensiva de todos los fenómenos; en la reducción mecanicista, no: los mecanismos de nivel inferior explican fenómenos diferentes.

Con respecto al carácter final de la explicación mecanicista, y adelantando el siguiente apartado (“Interdisciplinariedad”), cabe agregar la opinión de Thomas Brante sobre el objetivo explicativo de la ciencia. Brante (2008) señala que la ciencia puede ser retratada de diferentes maneras. Resalta tres de sus procederes básicos. Uno es la descripción, es decir, la medición precisa y la estimación meticulosa. Otro es la manera específica en que la ciencia divide su dominio de estudio en categorías y subclases: la taxonomía. La taxonomía determina la observación e identificación de los hechos significativos de una disciplina y provee los conceptos básicos entre los cuales las asociaciones y relaciones causales pueden establecerse. El tercer proceder es la explicación, que consiste entonces en relacionar, de determinadas maneras, conceptos con categorías.

La importancia de las descripciones precisas (la toma de datos exactos) es obvia. Pero la descripción es siempre “category-dependent”: se usan tipologías y aparatos conceptuales para clasificar e incluso producir descripciones de hechos. Sin explicaciones, sin una identificación de los mecanismos, las clasificaciones no son suficientes. Un ejemplo de ello, según Brante, es la astrología. Una explicación científica implica relacionar categorías, preferentemente determinando relaciones causales entre ellas. Y, si se encuentra el mecanismo que une causa y efecto, la relación causal es defendible^[21].

Por esto Brante sostiene que las explicaciones son “últimas” en ciencia: la descripción depende de la clasificación, y la clasificación requiere de la explicación para ser suficiente. Señala también que los grandes adelantos en ciencia usualmente involucran la identificación de mecanismos. Más allá de las descripciones están las causas y los mecanismos y son ellos los que deben examinarse para explicar por qué las cosas son lo que son. Brante señala la situación actual en sociología y otras ciencias sociales (con excepción, tal vez, de la economía): la fragmentación de los temas, la falta de una teoría explicativa sólida. En este sentido apunta su propuesta para que las ciencias sociales eleven sus ambiciones y se vuelvan ciencias explicativas. La persecución de un objetivo común por parte de todas estas disciplinas debería mejorar la estabilidad y solidez disciplinaria, y así permitir (o mejorar) la acumulatividad. Un objetivo común mejora las posibilidades de cooperación, de investigación interdisciplinaria, no solo entre las ciencias sociales, sino también entre ciencias sociales y ciencias naturales. Empleando un enfoque básico compartido, las áreas de interés común, como los mecanismos tras los desórdenes mentales humanos, deberían ser más fáciles de explorar de manera multidisciplinaria.

Para resumir, puede decirse que las ventajas de la explicación mecanicista sobre la explicación nomológico deductiva son:

Mayor flexibilidad de representación (no está limitada a la formulación proposicional).

Mejor transmisión de la información (por la flexibilidad de representación y las ventajas de la representación diagramática).

Mayor poder explicativo (brindan mejor comprensión al explicar el cómo; la animación mental de los mecanismos permite mejor comprensión que la inferencia lógica).

Mayor aplicabilidad (esto por dos motivos: por su flexibilidad de representación y por no requerir leyes, lo cual permite que el modelo pueda ser utilizado por diferentes disciplinas).

Son finales (en el sentido usual, ya que brindan una comprensión tal que no requiere ulteriores explicaciones, y en el sentido que plantea Brante, 2008, ya que permiten explicar las clasificaciones).

1.3. La explicación estadística

Como se dijo, una de las mayores limitaciones del modelo estándar de explicación científica es consecuencia del requisito R3: la presencia de al menos una ley en el explanans. En ciertas disciplinas se dispone comúnmente, ya no de leyes deterministas, sino de ciertas regularidades no estrictas (puede tratarse de leyes de índole probabilista, de leyes estadísticas, o de enunciados que describen correlaciones entre variables). No dicen que algo necesariamente acontecerá (como “el agua se expande al congelarse”), sino que algo acontecerá con un determinado grado de probabilidad (como “la que afirma la probabilidad del 0,51 de que en el género humano nazcan varones”^[22]). Estas regularidades no estrictas aportan cierta comprensión sobre los fenómenos, y pueden ser utilizadas para explicar. Cuando se utilizan enunciados que describen regularidades no estrictas en el explanans se tiene una explicación estadística^[23]. La explicación estadística es similar a la explicación nomológico deductiva, con la excepción del requisito R3^[24]. En la explicación nomológico deductiva no pueden aparecer estas generalizaciones no estrictas, dados R1 y R2^[25].

Un ejemplo de explicación estadística podría rescatarse del ejemplo desarrollado en el capítulo 2, §7: para explicar por qué una determinada persona desarrolló úlcera de duodeno, se dice que esa persona consumió regularmente aspirinas y que, aproximadamente, el 20 % de las personas que utilizan antiinflamatorios no esteroides, como la aspirina, desarrollan úlcera de duodeno.

Explicaciones estadísticas de este tipo son usuales, por ejemplo, en disciplinas como economía, sociología, medicina o biología. La diferencia esencial entre esta explicación y la nomológico deductiva no es formal, sino una consecuencia de la estructura formal: en la explicación estadística se rompe la simetría entre explicación y predicción. Si el 20 % de las personas que consumen aspirinas regularmente desarrolla úlceras, y una determinada persona consume regularmente aspirinas, no puede predecirse que contraerá úlcera de duodeno. A lo sumo, puede decirse que probablemente desarrollará úlcera de duodeno. De esta manera, la ocurrencia o no de lo predicho no sirve para evaluar los enunciados que componen la teoría.

La principal crítica que el neomecanicismo hace a este modelo de explicación^[26] es que no es final. Las explicaciones estadísticas requieren ulterior explicación porque recurren a una correlación entre variables sin explicar por qué están estas variables relacionadas. Las correlaciones estadísticas toman la forma de una descripción fenoménica: a ciertas condiciones iniciales (input) usualmente se siguen ciertas condiciones resultantes (output). Cómo y por qué se dan las condiciones resultantes queda sin explicación. Por ser “opaco” el proceso intermedio, se denomina a estas correlaciones “de caja negra” o “cajas negras”. Las explicaciones que apelan a cajas negras no son finales porque emplean enunciados que no fueron ellos mismos explicados. Una de las maneras de “abrir” las cajas negras es mostrar el mecanismo que, dadas las condiciones iniciales, produce las condiciones finales.

Una ventaja de las explicaciones mecanicistas sobre las estadísticas es señalada por distintos autores^[27]: uno de los problemas de la llamada “investigación cuantitativa” en ciencias sociales es el posible carácter espurio de las correlaciones entre variables. Como los mecanismos permiten abrir las cajas negras, es decir, permiten explicar y comprender cómo ciertos factores generan un resultado, son una herramienta especialmente útil para eliminar las correlaciones espurias. Buscar el mecanismo que, dadas ciertas condiciones, provoca un fenómeno es abrir la caja negra y entender por qué ocurre dicho fenómeno. Esto adelanta, en cierta forma, algo que se desarrollará más adelante en este capítulo (§3): los mecanismos no solo son una buena fuente de explicaciones, sino también una buena guía para la investigación.

Al proponer que los mecanismos ocupen un rol central en las ciencias sociales, no se propone abandonar la investigación cuantitativa y el intento de obtener teorías sociales de gran alcance. Se trata de intentar “descender de nivel” para encontrar qué causa los fenómenos de nivel macro: buscar los mecanismos que subyacen a ciertos cambios. Esos mecanismos dirán cómo se producen los cambios. En ciencias sociales, ese descenso de nivel puede darse de diferentes maneras. Tilly y quienes pertenecen a su escuela proponen bajar a un nivel medio y encontrar procesos robustos para explicar los fenómenos de historia social. Sociólogos y economistas tienen diferentes estrategias o teorías para abordar el nivel inferior: la teoría de la elección racional, la teoría funcionalista y la teoría del poder de la sociedad (Mahoney 2002; 2003). Es usual identificar al neomecanicismo (en ciencias sociales) con el reduccionismo de la teoría de la elección racional, pero esto es un error. De hecho, Boudon (1998) discute que la teoría de la elección racional sea la teoría adecuada para abrir las cajas negras a la manera neomecanicista. Su crítica se basa en ejemplos que muestran que la teoría de la elección racional puede fallar, como la paradoja de Allais (Allais, 1953; Allais y Hagen, 1979; Hagen, 1995), el ultimatum game (Hoffman y Spitzer, 1985; Wilson, 1993), la paradoja de la reacción excesiva (Mills, 1951) y la paradoja de Axelrod (Axelrod, 1990), entre otras. Boudon propone un modelo amplio, que incluye la teoría de la elección racional como un caso especial, y al cual denomina “modelo cognitivista” (cognitivist model)^[28]. También Hedström y Ylikoski (2010, p. 60) señalan que la explicación mecanicista no implica compromiso ni con la teoría de la elección racional ni con el individualismo metodológico, porque para una explicación mecanicista en ciencias sociales basta con unos pocos supuestos sobre deseos, creencias y oportunidades, y no requiere comprometerse con todos los supuestos teóricos y metodológicos de una teoría de la acción determinada.

En suma, el modelo de explicación mecanicista aventaja al modelo estadístico en que no utiliza cajas negras y, por ende, provee explicaciones finales. Y esto sin renunciar a la teorización y sin comprometerse necesariamente con la teoría de la elección racional o cualquier otra.

1.4. La explicación causal

El modelo de explicación estadística es usualmente presentado como un submodelo del estándar, por las similitudes entre ambos. Otro de los modelos explicativos presentados como submodelo del estándar es el causal. La diferencia entre el estándar y el causal consiste en un único punto, ya que en la explicación causal, el requisito R3 del modelo estándar es reemplazado por el siguiente:

R3’: El explanans contiene al menos una ley causal^[29].

En el caso de la explicación estadística, la flexibilización del requisito R3 hace que el modelo sea más aplicable, pero pierde fuerza explicativa, por lo cual las críticas al modelo estadístico no son tanto por sus limitaciones de aplicación sino, más bien, por las limitaciones del modelo mismo. En el caso de la explicación causal se da la situación contraria: el requisito R3’ hace que el modelo explique mejor, pero lo hace mucho menos aplicable.

La explicación causal es epistémicamente superior a la nomológico deductiva (en el ejemplo de la muerte de Sócrates, el explanans deberá contener la ley causal según la cual la cicuta causa la muerte de los seres humanos, y la condición inicial que dice que Sócrates bebió cicuta), pero las críticas a la necesidad de leyes es más fuerte, dado que se requieren leyes causales. Al igual que la caracterización de las leyes deterministas, la caracterización de leyes causales es problemática. En todo caso, la crítica al modelo es que las leyes causales son más escasas que las leyes deterministas, y en algunas disciplinas es, como se dijo, discutible incluso que existan tales leyes.

La explicación mecanicista empata la principal ventaja de la causal, ya que brinda el mismo tipo de comprensión (porque detalla en el explanans las causas del fenómeno descripto en el explanandum), y evita su principal dificultad, porque no requiere leyes de ningún tipo. En el parágrafo 4 de este capítulo se presentará el tratamiento de la causalidad que presenta el neomecanicismo.

1.5. Modelos explicativos alternativos

Bajo el rótulo de “modelos explicativos alternativos” se incluyen aquí algunos de los modelos explicativos que prima facie no requieren leyes^[30]. En este sentido, son alternativos al (y no submodelos del) modelo estándar, y por lo tanto las críticas que reciben son distintas.

Como se verá, los neomecanicistas sostienen que la explicación mecanicista es una buena alternativa frente al modelo estándar y aventaja, además, a los modelos alternativos que se comentarán aquí. Todos ellos comparten con el estándar la primacía (casi exclusividad) de la formulación lingüística o proposicional, por lo cual siguen valiendo frente a ellos las ventajas que se mencionaron en el apartado anterior, relativas a la flexibilidad representacional de la explicación mecanicista (con la consecuente ventaja en cuanto a la comprensión).

Dos de los modelos alternativos que se suelen comparar con la explicación mecanicista son propios de las ciencias sociales: la explicación por comprensión y la explicación por significación. Los demás modelos también están presentes en ciencias sociales, pero no son exclusivos de ellas: la explicación funcional, la explicación genética y la explicación teleológica. En la literatura reciben distintos nombres^[31], y diferentes trabajos se abocaron a la tarea de compararlos con la explicación mecanicista. Bunge (1997; 2004a; 2004b) contrapone la explicación mecanicista (además de a la explicación nomológico deductiva) a la explicación por comprensión o por significación^[32], la explicación funcional y la explicación teleológica. Tilly (2001b), y Tilly y Goodin (2006) contraponen en ciencias políticas, sociales y en historia, la perspectiva explicativa mecanicista a las perspectivas que denominan “escepticismo” (que sostiene que no es posible explicar los procesos políticos), “de leyes abarcantes” (que recurre al modelo nomológico deductivo y a submodelos de él que requieren leyes), “de propensión” (que recurre al modelo explicativo por comprensión o por significación) y “de sistema” (que recurre a la explicación funcional). Reskin (2003; 2005) opone la explicación mecanicista^[33] en sociología a lo que denomina explicación “por qué” (why): explicaciones que pretenden dar cuenta de las motivaciones de los agentes (y que usualmente toman la forma de explicaciones por comprensión y significación). A continuación, se exponen brevemente los modelos alternativos y las críticas que reciben.

El modelo de explicación por comprensión (Verstehen, por el término alemán para “comprensión”) y la explicación por significación son, como se dijo, modelos propios de las ciencias sociales^[34]. Grosso modo, explicar un fenómeno (social) por comprensión requiere reconstruir el estado mental de los individuos, como sus motivaciones, deseos, propósitos y oportunidades en el momento de la acción. Las acciones (y sus consecuencias) de los agentes (sean individuos, grupos u organizaciones) quedan explicadas cuando se entiende (merced al explanans) qué pretendían hacer en el momento de obrar. La principal limitación de este modelo radica en que supone la posibilidad de la empatía^[35]; es discutible que un sociólogo alemán del siglo XX pueda empatizar con un rey francés del siglo XV, o un adulto con un niño, por no mencionar el problema de la posibilidad de empatía con sociópatas o psicópatas.

Cuando se pretende salvar la estrategia evitando recurrir a la empatía, se intenta explicar por significación. En este modelo^[36], los objetos sociales, los individuos y los fenómenos sociales tienen significado: el mundo social es una red de significados, y esos significados son otorgados por las reglas sociales (que establecen también, entre otros, los modos correctos de acción y los roles de los actores). Estas reglas conforman una estructura que, por su naturaleza convencional, cambia todo el tiempo. Entender un fenómeno (social) consiste en comprender los conceptos esenciales que intervienen, como las motivaciones, deseos, propósitos u oportunidades de los individuos en el momento de la acción. Esto puede lograrse si se explicitan los significados y roles de actos e individuos. Y para captar los significados no se requiere empatía, sino una especie de “traducción” de un código (el que rige la sociedad en la que se da el fenómeno a explicar) a otro (el que rige la sociedad del investigador). En este sentido, no es necesaria la empatía, sino la “traducción” de códigos, algo parecido a lo que se requiere para entender lo que dice alguien que habla otro idioma. Al igual que las reglas gramaticales, las reglas que dan significación son convencionales y arbitrarias. No obstante, hay una diferencia importante: las reglas de las convenciones idiomáticas están explicitadas; los códigos sociales, no (al menos, no totalmente). Los códigos de la propia sociedad se adquieren por el hecho mismo de ser parte de esa sociedad y ocupar un lugar en esa red de significaciones. El problema es que comprender las significaciones de otra sociedad implica haber aprendido cuáles son las convenciones implícitas y explícitas de esa otra sociedad. Si no se requiere empatía para tal captación, habrá que hacerse del código de esa otra sociedad (por ejemplo, apelando a “traductores” que conozcan, aunque sea parcialmente, ambas sociedades). Ese código consta de reglas sociales que son enunciados generales con forma de ley, aunque con un dominio restringido: son aplicables solo a una sociedad, no son transculturales. Y si bien estas reglas no serán “leyes de la naturaleza”, sí serán enunciados legaliformes con aplicación no universal. Entonces, una explicación de este tipo puede reformularse como una forma de explicación nomológico deductiva, solo que no utilizará leyes “transculturales”, sino reglas culturales. De ser aceptable esta interpretación, sería una debilitación del requisito R3. Si la explicación por significación es implícitamente una explicación nomológico deductiva (o son explicaciones equivalentes), le caben a ambos modelos las mismas críticas. Con respecto a la aplicabilidad del modelo, las críticas no son las mismas, pero específicamente a la explicación por significación puede criticársele que es un modelo aplicable solo a fenómenos que acontecen en sociedades humanas.

La explicación mecanicista no requiere empatía ni traducción de leyes de ningún tipo. Requiere que se tenga identificado el mecanismo que causa el fenómeno (aunque, como se dijo, puede haber fenómeno sin que lo cause un mecanismo). Para modelar los mecanismos sociales que requieren modelar la acción, no son necesarias leyes: bastan unos pocos supuestos sobre los atributos de los agentes, sus deseos y sus oportunidades. Por eso, de tenerse identificado el mecanismo causante de un fenómeno, la explicación mecanicista será superior a la explicación por comprensión o por significación.

Otro modelo explicativo alternativo que suele oponerse a la explicación mecanicista es el de explicación teleológica por funciones o metas^[37], que no pretende explicar fenómenos de cualquier índole, sino que se limita a algunos biológicos y sociales. Los elementos imprescindibles para estas explicaciones son los sistemas (ya sean sociales, como manadas o sociedades humanas, o biológicos, como el respiratorio). La idea es que los sistemas subsisten merced a permanecer en un estado de “normalidad” u homeóstasis^[38]. La explicación funcional de un fenómeno (como la transpiración) consiste en mostrar cuál es el aporte de ese fenómeno al estado de equilibrio del sistema y por ende, a su supervivencia y conservación (el aporte de la transpiración consiste en bajar la temperatura corporal). Como señala Bunge (1997, p. 413), la explicación mecanicista tiene la ventaja de no apelar a conceptos como adaptación o equilibrio: ciertos fenómenos son desadaptativos, o antihomeostáticos (por ejemplo, los ataques terroristas o los movimientos revolucionarios).

Si se consideran las definiciones de sistema y mecanismo propuestas en el capítulo 3, se verá que las explicaciones funcionales pueden reformularse en términos de explicación mecanicista, pero no a la inversa. Dar una explicación funcional requiere un conocimiento del comportamiento del sistema, particularmente su interacción con otros sistemas, su comportamiento interno, las consecuencias que acarrea salir del estado homeostático y los límites dentro de los cuales el sistema debe mantenerse (sus estados). Si se dispone de toda esta información, se estará en condiciones de dar una explicación mecanicista. Y hay ciertos fenómenos (no evolutivos o no sociales, como el plano inclinado) que no son explicables con el modelo funcional y lo son, en cambio, con el modelo de explicación mecanicista. El modelo de explicación teleológica por funciones y metas parece ser un submodelo del mecanicista (o, en todo caso, parece que es posible reconstruir toda explicación teleológica por funciones y metas de manera tal que resulte una explicación mecanicista).

El modelo de explicación teleológica por propósitos e intenciones^[39] es un modelo propuesto para algunos fenómenos resultantes de la conducta: para explicar por qué alguien hizo algo, se muestra qué es lo que ese agente pretendía y cómo pensaba lograrlo (y, tal vez, por qué no hizo otra cosa). Este tipo de explicación se utiliza usualmente para explicar fenómenos históricos (por ejemplo, si se quiere explicar por qué determinado gobierno tomó ciertas medidas económicas se dice que quería contener la inflación), pero lo cierto es que puede usarse también para explicar fenómenos de conducta animal (por ejemplo, puede decirse que el pez espinoso, en el ritual de apareamiento, se mueve en zigzag “para” atraer la atención de la hembra). Claramente, este modelo de explicación tiene la ventaja de ofrecer cierta comprensión del fenómeno que se desea explicar. No obstante, tiene el mismo problema que la explicación por comprensión: el acceso a la mente del agente. Cuando la explicación teleológica por propósitos e intenciones no puede ser llevada a una explicación mecanicista (por ejemplo, porque no se dispone de un modelo mecanicista lo suficientemente desarrollado), la explicación mecanicista puede resultar un complemento valioso: por ejemplo, Bunge (1997, p. 413) señala que conocer (o conjeturar) los propósitos de los agentes es solo parte de la tarea, porque también se deben conocer (o hipotetizar) los mecanismos que, de operar, generarían el resultado deseado (retomando el ejemplo de las medidas de gobierno: es necesario saber cómo operan los mecanismos que reducen o frenan la inflación, y de los que pretende valerse el gobierno para lograr su objetivo).

Un modelo de explicación utilizado comúnmente para explicar fenómenos que dependen de sus estados pasados (todos los procesos geológicos e históricos, y algunos fenómenos evolutivos, biológicos o sociales) es el modelo de explicación genética^[40], en el cual los autores neomecanicistas todavía no han reparado (Hasrun, 2011a). En este modelo explicativo^[41], el explanans consta de un grupo de proposiciones, E1, E2,…, En–1, que describen sucesivas etapas de un proceso continuo que desemboca en el fenómeno descripto en el explanandum, En. En una explicación genética adecuada, cada enunciado Ei describe un hecho Hi que es consecuencia de otro hecho, Hi–1, descripto en el enunciado Ei–1, de manera que el explanans consiste en la descripción de una cadena causal en la que lo descripto por cada enunciado es consecuencia de lo descripto por el enunciado anterior (excepto, por supuesto, E1) y el último eslabón de la cadena causal es el fenómeno a explicar. Por ejemplo, para explicar por qué hay un lago determinado en medio de una montaña, se describen las etapas del proceso (posterior a la formación de la cadena montañosa) de glaciación que dan origen al glaciar (grosso modo: el cambio climático forma el glaciar, que por su peso forma una depresión; al retirarse el glaciar, el agua queda acumulada en la depresión, formando el lago). Nótese que este modelo explicativo, que pretende no recurrir a leyes de ningún tipo, parece especialmente adecuado para explicar fenómenos singulares en los cuales la historia previa del sistema es relevante (por ejemplo, al explicar cómo se ha formado un organismo de crédito internacional no se pretende explicar cómo se forman los demás organismos de crédito internacional, sino solo ese). Es por esto que suelen emplearse explicaciones genéticas para explicar fenómenos históricos como, por ejemplo, la renuncia de un determinado presidente. Se dice, por ejemplo, que el presidente tomó una serie de medidas económicas que afectaron especialmente a la clase media y baja, que esas medidas generaron descontento y comenzaron manifestaciones, que el presidente ordenó reprimirlas, que la represión originó más manifestaciones y descontento, y la gente comenzó a exigir la renuncia del presidente quien, finalmente, renunció. Una de las críticas a este modelo consiste en señalar la dificultad de elegir los hechos relevantes en el proceso. En efecto, de todas las cosas que sucedieron desde la primera etapa hasta la última, se seleccionan solo algunas (en el caso del lago, no se menciona, por ejemplo, lo que acontecía simultáneamente en otras regiones –como en la línea del Ecuador, que no resultó afectada por la glaciación– o las horas de luz solar diarias que recibía el glaciar que se encontraba sobre el lago, porque no es relevante a la formación del lago; y en el caso de la renuncia del presidente, no se menciona, por ejemplo, que cierto actor se divorció o que estaba a punto de terminar un ciclo lectivo cuando se ordenó la represión). La principal crítica al modelo genético es, pues, que o bien la selección de los hechos causalmente relevantes es arbitraria, o bien hay algún tipo de regularidad (por ejemplo, de tipo estadístico) que establece qué es causalmente relevante y qué no. Es decir, las distintas etapas del proceso que se describen en la explicación estarían conectadas por algún tipo de regularidad, de manera que los enunciados explanantes que describen esas etapas pueden ser vistos como explicaciones estadísticas (o probabilísticas) incompletas, con premisas (que contienen leyes del algún tipo) implícitas^[42]. Según esta crítica, con E1 y algunas premisas implícitas se explicaría (con el modelo estadístico o probabilista) E2, con E2 y algunas premisas implícitas se explicaría E3, y así se podría seguir hasta llegar a E.

Claramente, la explicación mecanicista no es una explicación genética. Lo que hasta ahora no se ha notado y se propone aquí, es que, si la comprensión del fenómeno requiere una explicación genética, la explicación mecanicista, de ser posible, brinda una mejor comprensión del fenómeno y presenta una solución a la crítica de las condiciones relevantes. Debe tenerse en cuenta algo que ya se ha dicho en más de una oportunidad sobre uno de los supuestos del neomecanicismo: no todo fenómeno es causado por un mecanismo y, por ende, el modelo de explicación mecanicista no puede utilizarse para explicar todos los fenómenos. Por eso, si existe (si se tiene debidamente identificado) un mecanismo que causa el fenómeno que se pretende explicar, entonces la explicación mecanicista tiene tres ventajas sobre la genética, a la vez que mantiene el poder explicativo: (a) brinda una mejor explicación, por todo lo dicho sobre las ventajas respecto de la flexibilidad de soporte, y porque no solo permite ver las etapas intermedias, sino también cómo las relaciones entre unidades generan esas etapas; (b) identificar un mecanismo, como se dijo, es identificar las unidades, relaciones, modus operandi, etc.: si se ha identificado el mecanismo, se sabrá qué es lo que la explicación genética debe contener en el explanans, se dispondrá de un criterio para seleccionar, de entre todo lo que sucede, aquello que es relevante para el resultado final. Porque lo relevante será, justamente, solo aquello que intervenga en (o sea consecuencia de) la operación del mecanismo. La tercera ventaja del modelo mecanicista sobre el genético es (c) la posibilidad de explicar no solo fenómenos singulares, sino también generales. Es decir, cuando se tengan explicaciones aceptables para un fenómeno, una genética y una mecanicista, la mecanicista tendrá mayor posibilidad de generalizarse. Piénsese, por ejemplo, en la explicación de fenómenos históricos, para los cuales la explicación genética parece especialmente apta: no hay generalización posible en el modelo genético; solo pueden explicarse los fenómenos particulares, uno por uno. Por ejemplo, cada proceso de democratización debe explicarse genéticamente como un caso aislado, y la explicación de la democratización en un país no servirá para explicar la democratización en otro, porque cada país tiene su propia historia. La explicación genética sobre la formación de un lago no serviría para explicar la formación de ningún otro lago. Una explicación mecanicista permite emplear, por ejemplo, los mecanismos de democratización (capítulo 2, §6) para explicar los procesos de democratización en distintos países o en distintas épocas, superando así el nivel de lo particular, aunque posiblemente los mecanismos de democratización no permitan explicar todos los procesos de democratización que han sucedido (es decir en todos los países y en todas las épocas).

En suma, la explicación mecanicista presenta ventajas frente a los demás modelos de explicación científica, tanto frente a los modelos propuestos para todas las ciencias y todos los fenómenos, como frente a aquellos modelos propuestos solamente para algunas disciplinas o algún tipo de fenómeno. Pero de lo dicho aquí no debe entenderse que la propuesta es dejar de lado o abandonar los demás modelos de explicación por considerarlos inadecuados o inaplicables. Simplemente se ha pretendido señalar los límites de los demás modelos explicativos y resaltar las virtudes de las explicaciones mecanicistas per se y frente a los demás modelos. Pero, claramente, si no todo fenómeno es causado por un mecanismo –como se sostiene aquí–, no todo es explicable empleando el modelo mecanicista.

Recuérdese que no se han analizado todos los modelos explicativos, por lo cual no se ha mostrado que la explicación mecanicista sea la mejor disponible. Tener presente este punto es importante, porque el neomecanicismo se propone como un enfoque complementario (al menos así se lo considera aquí) y como tal, no es necesario que la explicación mecanicista sea ventajosa respecto de todos los demás modelos, sino que, en tanto modelo complementario, sea fructífero. Ahora bien, si el neomecanicismo se propusiera como enfoque alternativo (dado que en algunas disciplinas específicas, como la neurociencia, la propuesta parece ir en ese sentido), debería mostrar la superioridad de su modelo explicativo frente a todos los demás modelos.

2. Interdisciplinariedad

Un aspecto interesante de la propuesta neomecanicista es la posibilidad de investigación interdisciplinaria. No es, por supuesto, la única manera de investigación interdisciplinaria. Lo que el neomecanicismo tiene como ventaja es que es relativamente fácil identificar los accesos a la interdisciplinariedad. Por ejemplo, reconocer que en un determinado sistema concreto (un glaciar, una población de gaviotas, el personal de una empresa) opera un mecanismo permitiría que otra disciplina interesada en el mismo sistema concreto (o en sistemas similares) investigue el mecanismo. Esto será más fácil en la medida en que el mecanismo gane generalidad (o grado de abstracción). Cuando distintas disciplinas comparten un objeto de estudio, usualmente los supuestos teóricos de cada disciplina resultan un impedimento para el trabajo interdisciplinario, dado que las teorías suelen no ser totalmente compatibles. La investigación basada en mecanismos no enfrenta este problema por dos motivos (Hedström y Ylikoski, 2010, p. 61): en primer lugar, los mecanismos no tienen por qué organizarse formando una gran teoría, con lo cual, si dos mecanismos parecen irreconciliables lo único que importa es identificar en cada caso concreto cuál de los dos opera; en segundo lugar, la modelación de mecanismos (incluso la modelación de mecanismos sociales, usualmente muy complejos) requiere pocos supuestos, es decir, apenas los supuestos mínimos sobre las características de las unidades. Lo único que se necesita, entonces, es que los supuestos mínimos con los cuales se modelan los mecanismos no sean incompatibles con las teorías. Si, además, los mecanismos son compatibles entre sí, se logra un conjunto de herramientas, una red de mecanismos útiles para las distintas disciplinas.

Una manera de encontrar acceso a la interdisciplinariedad consiste en la comparación de los cambios en los sistemas: si, por ejemplo, los cambios que provoca en un sistema un mecanismo debidamente identificado son similares a los cambios observados en otro sistema, es probable que el mecanismo identificado tenga interés también para la disciplina que estudia este segundo sistema. Aquí puede mencionarse la importancia de la imitación en la conducta^[43]: los mecanismos que subyacen a la conducta animal imitativa podrán ser investigados por científicos sociales. Estas similitudes en los estados finales generados por los mecanismos no garantizan que la interdisciplinariedad resulte exitosa o fructífera, ya que el mecanismo no necesariamente será el mismo, pero señalan espacios concretos donde la interdisciplinariedad puede darse.

Brante (2008) señala que poseer un objetivo común, como la identificación de mecanismos, aumenta las posibilidades de cooperación entre las disciplinas, no solamente entre las ciencias sociales, sino también entre las ciencias sociales y naturales, como por ejemplo, entre la biología y la neuropsiquiatría, disciplinas que pueden aunar su investigación tras la identificación de los mecanismos que subyacen a fenómenos como los desórdenes mentales.

Otra forma de facilitar la interdisciplinariedad sería poseer un lenguaje común (a las distintas disciplinas que interactúen o cooperen) que permitiera capturar las relaciones y sus resultantes (es más fácil poseer un lenguaje común para referirse a los demás elementos del mecanismo). Como se dijo en este capítulo (§1.2), una de las ventajas de la explicación mecanicista es la flexibilidad de representación, heredada de la flexibilidad en el momento de la conceptualización de los mecanismos, es decir, la explicación es flexible por la libertad en la elección de herramientas para modelar un mecanismo. Las relaciones entre unidades, particularmente las interacciones y sus resultantes, pueden ser capturadas, por ejemplo, por funciones matemáticas, juegos extensivos, juegos evolutivos o juegos cíclicos. La teoría de juegos, por ejemplo, puede proveer un lenguaje para capturar las relaciones, propiedades e interacciones de y entre las unidades de un mecanismo, y proveer modelos mecanicistas que sirvan a diferentes disciplinas. Para desarrollar este punto con más detalle, puede tomarse como ejemplo un juego evolutivo, y mostrar la manera en que permite modelar un mecanismo. La idea es que ese juego (que modela un mecanismo) podrá ser utilizado para explicar diferentes fenómenos de diferentes disciplinas.

En Hasrun (2008) se propone que ciertos mecanismos sociales (mecanismos macro-macro^[44]) pueden modelarse utilizando teoría de juegos evolutivos. Siguiendo lo propuesto por Baldassarri (2005)^[45], la modelación de mecanismos sociales debe considerar los múltiples niveles de agregación, los períodos de normalidad y anormalidad, y la dinámica histórica. Tomando un ejemplo de juego evolutivo, en Hasrun (2008) se propone que juegos de este tipo permiten modelar mecanismos macro-macro de manera satisfactoria. No se desarrolla el ejemplo en detalle, como se hará a continuación, pero se presenta la doble propuesta: existen mecanismos macro-macro, y algunos juegos evolutivos pueden ser vistos como modelos mecanicistas.

La teoría de juegos evolutivos es una rama o parte de la teoría de juegos, originalmente desarrollada por Maynard Smith (1982) para mostrar que la teoría de juegos puede aplicarse a la conducta animal. El lugar central de la teoría en el trabajo inaugural es ocupado por la selección natural: el proceso de supervivencia del mejor adaptado (junto con las mutaciones) es usado para modelar las frecuencias con las cuales diferentes estrategias son representadas en la población con el transcurso del tiempo. En un modelo evolutivo típico, los jugadores son previamente “programados” para ciertas estrategias y son pareados azarosamente con otros jugadores en encuentros repetidos de a pares. La frecuencia relativa de una estrategia en una población es simplemente la proporción de jugadores de esa población que adoptan esa estrategia. Los juegos evolutivos permiten modelar juegos en los que se ve la manera en que cambian con el tiempo los perfiles de estrategia de las poblaciones, puesto que los resultados de los juegos en un momento dado determinan la frecuencia de las diferentes estrategias en el futuro.

En la teoría de juegos clásica los jugadores tienen conjuntos de estrategias de los cuales eligen estrategias particulares. En los juegos evolutivos la sociedad tiene un conjunto de estrategias (el conjunto de formas culturales alternativas) y los individuos heredan o eligen de ese conjunto las estrategias que jugarán en las interacciones estratégicas. El concepto de equilibrio de los juegos clásicos es reemplazado en los juegos evolutivos por el de estrategia evolutivamente estable: una forma cultural es una estrategia evolutivamente estable si, una vez adoptada por todos los miembros de la sociedad (firma, familia, o institución), ningún pequeño grupo de individuos usando una forma cultural alternativa puede invadir. Puede interpretarse un juego evolutivamente estable como una competencia entre reglas o características (y no entre los individuos portadores de esas características): las características ventajosas se autorreplicarán, es decir, las características o estrategias “ganadoras” serán copiadas y “eliminarán” a las características o reglas menos ventajosas. En cualquier caso, y dejando a un lado la discusión sobre qué es, hay algo que se transmite o permanece y se lo denomina, simplemente, replicador: en los juegos evolutivos existen estrategias, características, reglas o rasgos que se replican a sí mismas y que determinan las conductas estratégicas en el juego.

Los juegos evolutivos presentan una dinámica del replicador. Se asume que la porción de una población que alberga un determinado replicador se incrementa con una taza proporcional a dos factores: por una parte, el porcentaje (la fracción) de la población que alberga al replicador y, por otra parte, la diferencia entre la adaptación actual de los portadores del replicador y la adaptación promedio de todos los portadores de la población.

No todos los equilibrios son igualmente estables en juegos evolutivos; estos juegos presentan equilibrios con mayor o menor “estabilidad”. Los equilibrios más estables serán aquellos que se autocorregirán ante un eventual cambio o variación repentina. A los menos estables no se vuelve tras una variación: tras la variación, la dinámica lleva a otro equilibrio distinto.

El ejemplo que se analizará aquí es el modelo de segregación residencial que presenta Bowles (2006, cap. 2): muestra cómo la modelación de un juego evolutivo muestra que, aunque los individuos prefieran vivir en un barrio mixto, la dinámica del replicador (que muestra cómo resultan las relaciones de compra-venta de propiedades en cada momento) hace que el barrio termine segregado^[46].

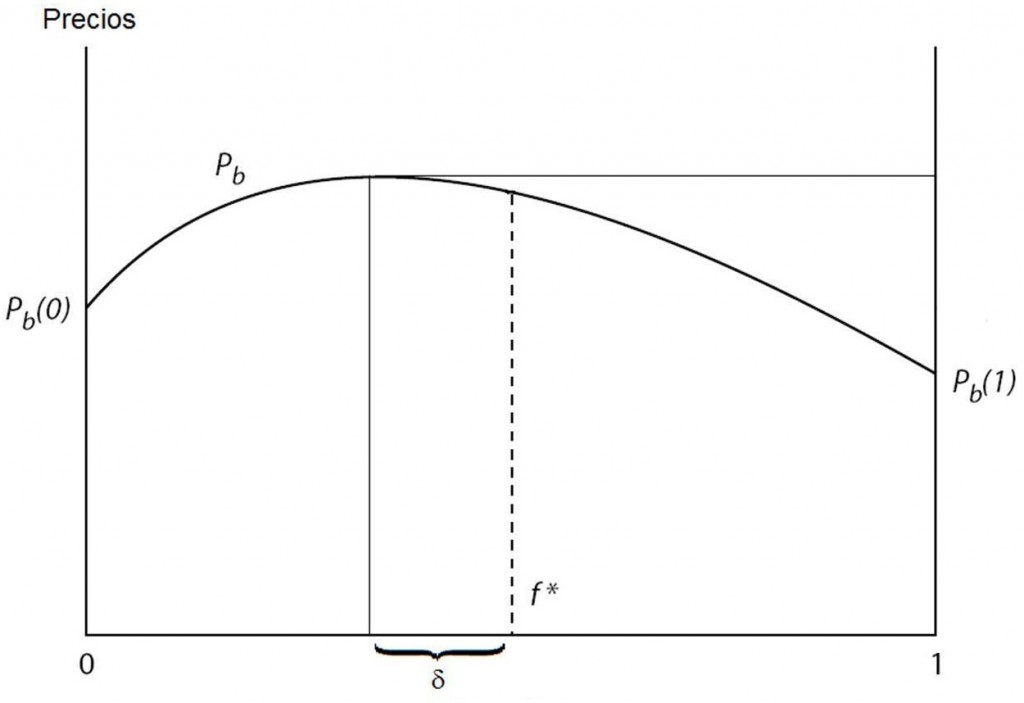
Considérese un barrio en el cual todas las unidades habitacionales son igualmente deseables para todos los miembros de la población. Las preferencias de los individuos sobre vivir en este barrio dependen solamente de la composición racial del barrio. En este barrio y en la población que lo rodea, los “verdes” (g) y “azules” (b) prefieren vivir en un barrio mixto, aunque prefieren que su propio grupo supere en número, por una fracción, al otro. Estas preferencias serán expresadas por el precio que los verdes (p_g) y el precio que los azules (p_b) estarían dispuestos a pagar por una propiedad en el barrio, dependiendo en cada caso de la fracción de propiedades en el barrio ocupadas por verdes, f ∈ [0, 1] (la fracción de propiedades ocupadas por azules será, por ende, 1 – f). Sea p el precio intrínseco de propiedades similares. Lo que interesa reflejar en la preferencia es cuánto por encima de p se está dispuesto a pagar por una casa, dependiendo de la composición del barrio en el cual la propiedad se encuentra. Las ecuaciones (A) y (B) muestran las preferencias de los grupos, siendo p una constante positiva, f ∈ [0, 1] y δ ∈ (0, ½):

(A) p_b (f) = ½ (f + δ) – ½ (f+ δ)² + p

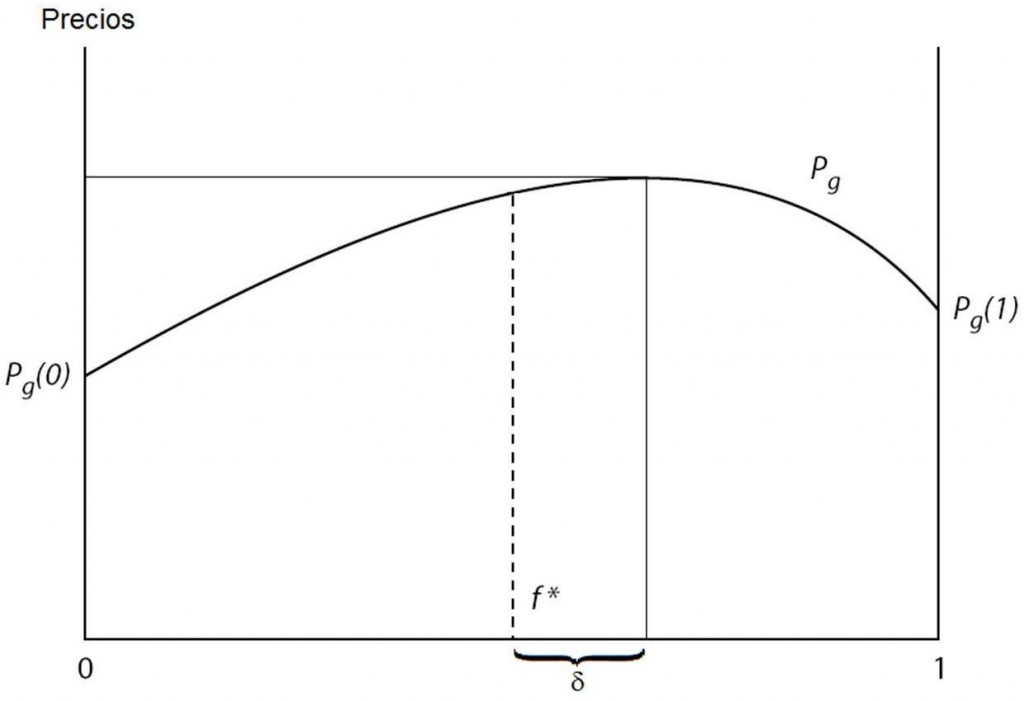
(B) p_g (f) = ½ (f – δ) + ½ (f – δ)² + p

La función (A) describe las preferencias de los azules: el precio que estarían dispuestos a pagar los azules en función de la composición de verdes (f) que rodea la propiedad. La figura 14.1 muestra la gráfica de esta función. En esta gráfica, el eje de las abscisas representa la composición del barrio en términos de los verdes: a la izquierda, el valor 0 indica un barrio sin verdes, es decir, totalmente azul; a la derecha, el valor 1 indica un barrio totalmente ocupado por verdes. El eje de las ordenadas muestra el precio que se está dispuesto a pagar. f* indica el valor medio en la distribución, es decir, es el punto en el cual el barrio es perfectamente mixto. Como puede verse, el precio más alto que un azul estaría dispuesto a pagar por una propiedad se encuentra a la izquierda de f*: en ½ – δ. El precio que un azul está dispuesto a pagar disminuye a medida que la composición racial toma los valores extremos 0 y 1. En 0 (barrio azul), el precio es más alto que en 1 (barrio verde): es decir, aunque prefieren vivir en un barrio casi mixto, si se les ofrecen propiedades en un barrio homogéneo, un azul estaría dispuesto a pagar más por un barrio homogéneo del propio grupo.

La función (B) describe las preferencias de los verdes. La figura 14.2 es el gráfico de esta función. El valor máximo aquí está dado en f* + δ, es decir, los verdes prefieren un barrio mixto con leve mayoría de verdes. Ese precio decae a medida que el barrio se va homogeneizando y en los extremos prefieren un barrio ocupado solamente por verdes (f = 1) a uno ocupado únicamente por azules (f = 0).

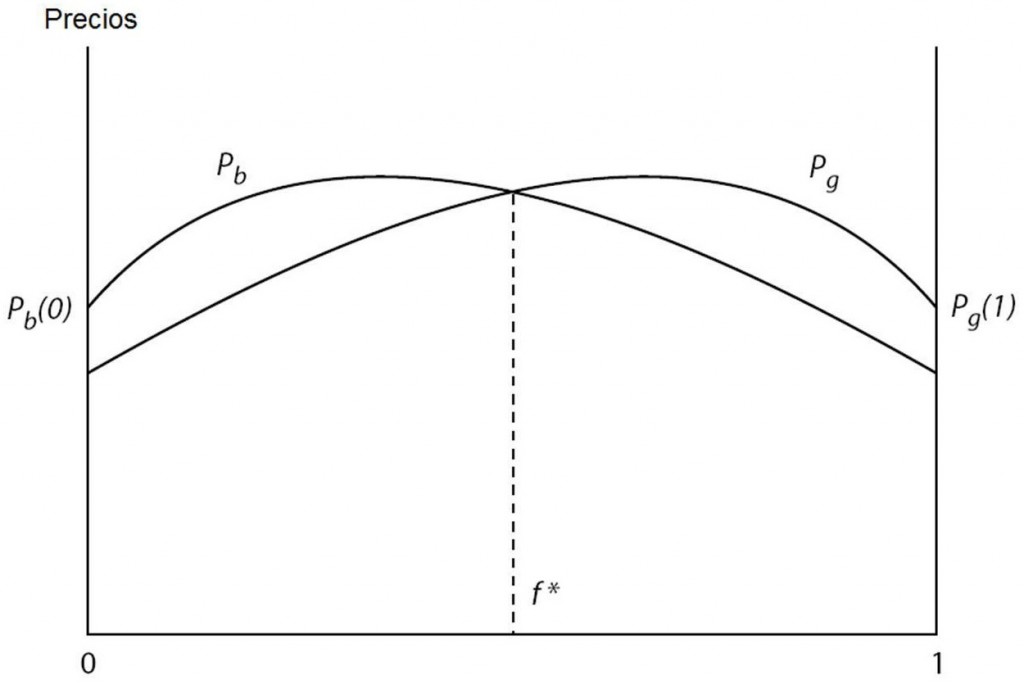
Si se derivan las dos ecuaciones con respecto a f, y se las iguala luego a 0, se obtienen los máximos de la función. Así puede verse que el barrio ideal para los verdes (el máximo de p_g) está compuesto de ½ + δ verdes, y el barrio ideal para los azules (el máximo de p_b) está compuesto por ½ – δ verdes. Estas preferencias no necesariamente son iguales: cada grupo podría tener su propia diferencia, o bien un grupo no prestar atención en lo absoluto a la composición racial y el otro sí. En el ejemplo, la diferencia entre los dos barrios ideales (en términos de fracción de verdes) es 2 δ; en otras palabras, para pasar de la composición barrial ideal de un grupo a la composición barrial ideal del otro grupo, se debe variar la composición primero en δ para llegar al punto medio, y luego otra vez δ para alcanzar el otro ideal. Por esto Bowles (2006, p. 66) se refiere a δ como “el grado de gustos discriminatorios de las dos clases” (the extent of discriminatory tastes of the two types). Para simplificar, el tamaño del barrio es normalizado con la unidad, de modo que f es, indistintamente, la fracción y el número de verdes.

 

Ahora bien, en cada período de tiempo hay en el barrio un número α de dueños (verdes y azules) que ponen en venta su propiedad. Los potenciales compradores forasteros visitan el barrio en la misma proporción que la población del barrio en ese momento (por lo que habrá, en total, f compradores verdes y 1 – f compradores azules). Los vendedores azules y verdes, y los potenciales compradores azules y verdes, se cruzan al azar.

Las transacciones entre comprador y vendedor del mismo grupo no cambian la composición del barrio. Lo interesante, lo que hará cambiar la composición son las transacciones entre gente de distintos grupos: un verde que le compra una propiedad a un azul o un azul que compra la propiedad de un verde. En cada período de tiempo, el número de vendedores verdes es α f (el número de vendedores multiplicado por la fracción de verdes). Y el número de vendedores verdes que son contactados por un potencial comprador azul en cada período es:

α f (1 – f)

Esto es, debe multiplicarse el número de vendedores verdes, α f, por el número de compradores azules, que será 1 – f, ya que la composición de compradores es idéntica a la composición barrial (f verdes y 1 – f azules). La probabilidad de que un vendedor azul se reúna con un comprador verde es idéntica: α (1 – f) f.

En cada período de tiempo, cada vendedor se entrevista solo con un potencial comprador, se lleve a cabo o no la transacción. La probabilidad de que se efectúe la venta depende de la diferencia entre la valuación de la propiedad que el comprador y el vendedor hacen; en otras palabras, depende de si la valuación del comprador es mayor de acuerdo con las ecuaciones (A) y (B). Si un potencial vendedor azul se encuentra con un potencial comprador verde, y f es tal que p_g > p_b, entonces la probabilidad de que la venta tenga lugar es β (p_g – p_b), donde β es una constante positiva que expresa la relación entre la diferencia de precio y la probabilidad de la venta.

Lo que interesa aquí es la evolución en el tiempo de la distribución de los grupos en el barrio, es decir, la evolución en el tiempo de f. Si en el instante t_i la composición barrial es f, en el instante t_{i + 1} la composición barrial será f’, dependiendo del resultado de una ronda de transacciones de compra-venta. f’ es una función de f: se debe restar a f (que es el número o la fracción de verdes) las propiedades compradas por azules y sumar las propiedades compradas por verdes (las transacciones entre iguales, como ya se dijo, no cuentan porque no alteran la composición barrial). Pero como las transacciones dependen de la composición barrial, solo un tipo de transacción resultará: o bien los verdes le venden a azules (porque 1 – f > f y, por ende, p_g < p_b) o bien los azules le venden a los verdes (porque f > 1 – f y, por ende, p_g > p_b). La ecuación que refleja esto es:

(C) f’ = f – α f (1 – f) r_b β (p_b – p_g) + α (1 – f) f r_g β (p_g – p_b)

con r_b= 1 si p_g < p_b y es 0 en todo otro caso; y r_g = 1 si p_g ≥ p_b y 0 en todo otro caso. r_b + r_g = 1. En la ecuación, r determina si se suman nuevas propiedades verdes o se restan nuevas propiedades azules: si la composición residencial favorece la transacción azul-verde (esto es, hay más verdes en el barrio y por eso los verdes están dispuestos a pagar un precio más alto que el precio intrínseco), habrá más residentes verdes y debe sumarse el tercer término (pero no restarse el segundo), por eso r_g toma el valor 1 y r_b toma el valor 0.

El segundo término de la ecuación (C) resta a f las nuevas propiedades azules (de haberlas): el número de nuevas propiedades será el producto de los vendedores azules que se reúnen con compradores verdes, α f (1 – f), multiplicado por la probabilidad que la venta azul-verde tenga éxito: β (p_b –  p_g), multiplicado por r_b que será 1 o 0. De manera análoga puede interpretarse el tercer término de la ecuación.

La variación en la composición residencial entre dos instantes, Δf, es la diferencia entre f’ y f: Δf = f’ – f. Es decir:

Δf = f’ – f = [f – α f (1 – f) r_b β (p_b – p_g) + α (1 – f) f r_gβ (p_g– p_b)] – f

Restando f se obtiene:

Δf = – α f (1 – f) r_b β (p_b – p_g) + α (1 – f) f r_g β (p_g– p_b)

Tomando en la parte derecha de la igualdad como factor común “α f (1 – f) β”, se obtiene:

Δf = (α f (1 – f) β) (– r_b (p_b – p_g) + r_g (p_g– p_b))

Distribuyendo “– r_b (p_b – p_g) + r_g (p_g– p_b)” se obtiene:

Δf = (α f (1 – f) β) (– r_b p_b + r_b p_g + r_g p_g – r_g p_b)

Tomando en “– r_b p_b + r_b p_g + r_g p_g – r_g p_b” los términos de a pares, y tomando como factor común – p_b para el par “– r_b p_b  – r_g p_b” y p_g para el par “r_b p_g + r_g p_g” se obtiene:

Δf = (α f (1 – f) β) (– p_b (r_b+ r_g) + p_g (r_b + r_g))

Dado que, como se dijo, r_b+ r_g = 1, se obtiene finalmente una ecuación más simple para Δf:

(D) Δf = α f (1 – f) β (p_g – p_b)

De esta ecuación puede verse que Δf = 0 si p_g = p_b, si f = 1 o si f = 0. Es decir, no hay variación en la composición residencial si no hay ventas (porque para que haya transacción el precio del comprador debe ser mayor al del vendedor), o si la composición barrial es homogénea (porque solo visitarán compradores del mismo tipo).

La ecuación (D) es una ecuación llamada “ecuación de la dinámica del replicador”.

El precio promedio, p, puede definirse de la siguiente manera:

(E) p = f p_g + (1 – f) p_b

Reacomodando la ecuación (D) se obtiene:

Δf = α f β (1 – f) (p_g – p_b)

Multiplicando 1 – f y p_g – p_b se obtiene:

Δf = α f β ((1 – f) p_g – (1 – f) p_b)

Multiplicando 1 – f por p_g se obtiene:

Δf = α f β (p_g – f p_g – (1 – f) p_b)

Reemplazando f p_g – (1 – f) p_b por p, de acuerdo a la definición (E), se obtiene otra formulación de (D):

(D’) Δf = α f β (p_g – p)

Un valor estacionario se define como un equilibrio estable si un cambio exógeno en f produce (por la dinámica del replicador) un Δf de signo contrario, es decir, si dΔf/df < 0. Si vale esta desigualdad, todo cambio en f se autocorregirá. La figura 14.3 muestra el comportamiento de las funciones de verdes y azules.

Como puede verse en la figura 14.3, existe un equilibrio en la composición mixta 50/50 (puesto que p_g = p_b, resulta que Δf = 0) pero ese equilibrio no es estable, porque dΔf/df > 0. Por no ser estable, un pequeño desplazamiento de la distribución 50/50 no se autocorregirá, sino que irá acumulándose hasta llevar a un barrio completamente segregado.

Para δ < 1/4 tanto verdes como azules preferirán el barrio integrado al segregado, incluso cuando el barrio segregado esté compuesto únicamente por individuos de su tipo: esto puede verse porque p_b (1/2) = p_g (1/2) > p_g (1) = p_b (0).

Así, los equilibrios estables que se esperan (los del barrio segregado) son los únicos resultados durables de esta interacción y son Pareto-inferiores a los barrios con composición integrada. En otras palabras, los equilibrios estables son resultados no deseados y no planeados.

Es fácil mostrar que la segregación completa (de cualquier tipo) es un equilibrio estable. La composición que exhibirá un vecindario es históricamente contingente: por ejemplo, si en el pasado reciente f fue menor que f*, lo esperable es que en el futuro f = 0.

En pocas palabras, lo que se muestra en la figura 14.3 es que se tienen tres equilibrios: los dos extremos (donde el barrio termina con una conformación común, es decir, se da la segregación) y el punto medio (con un barrio perfectamente mixto). Y estos equilibrios no son igualmente estables: el punto medio es menos estable que los extremos. Una manera de ver esto es seguir las curvas de las funciones en el gráfico. Si el barrio súbitamente cambia en su composición (por ejemplo, por un terremoto) lo que pasa en la gráfica es que se mueve la posición horizontal (por ejemplo, se pasa de f* a un lugar más cercano a 0, o de 3/4 se pasa a 5/8), con lo cual cambian los precios (las alturas de p_b y p_g), y puede verse que las curvas de los precios llevan más fácilmente a los extremos que al centro. Esto equivale a decir que si se está en los extremos de segregación y algo cambia súbitamente el estado del barrio, la dinámica hará volver el barrio a esa posición. Por el contrario, cualquier salida del punto medio (no las mínimas, pero cualquier desvío no despreciable) hará que el desvío continúe en su mismo sentido, hacia el extremo del barrio segregado.

Hasrun (2008) muestra que juegos de este tipo permiten modelar mecanismos sociales macro-macro, ya que al modelar los juegos se está dando una caracterización (aunque de manera indirecta) de los individuos, de las relaciones entre individuos y de las estructuras resultantes de esa interacción. Es decir, se cumplen los requisitos necesarios para la explicación de los fenómenos de interacción social (ver este capítulo, §1.2). En efecto: para modelar el juego han de suponerse cómo son los jugadores (en otras palabras, cuáles son sus preferencias y oportunidades), cómo son las interacciones y qué resulta en cada caso de ellas, y las reglas que se impongan al juego reflejan las instituciones (al menos, permiten reflejar algunas de sus características). Del juego surgirán los períodos de normalidad: los equilibrios en los que se juegan estrategias evolutivamente estables. Los juegos permiten, además, calcular el efecto de las anormalidades (qué ocurriría en determinado estado normal de la sociedad si la población cambiara súbitamente, es decir, si cambiara la proporción de jugadores que juegan cierta estrategia). Y la dinámica temporal está contemplada por la dinámica del replicador que establece los cambios por período de juego: bastará, pues, con establecer la tasa de interacción respecto de otros juegos, por ejemplo, para marcar la diferencia temporal. Este juego claramente modela un mecanismo macro-macro (es decir, de un tipo que no está contemplado en la clasificación expuesta en el capítulo 4, §2): dado el estado inicial del nivel macro (la composición barrial) y merced a la resultante de interacción (en este caso, la interacción es del tipo compra-venta, que en el ejemplo es modelada de cierta manera, y con una resultante que depende del contexto), el mecanismo muestra cómo se llegará a un resultado (posiblemente, a un barrio segregado, que es un estado Pareto-inferior). Este juego evolutivo permite explicar otros fenómenos, como por ejemplo por qué ciertos espacios (como plazas, parques, playas, paseos de compra o escuelas) muestran algún tipo de segregación (por estatus social, edad, conformación familiar o nivel de educación) incluso en contra de las preferencias de quienes ocupan esos espacios^[47].

Además, las explicaciones que utilizan estos mecanismos macro-macro son explicaciones finales (no apelan a cajas negras) aunque no de manera directa porque, aunque explican mediante la mecánica del juego cómo resultan ciertas instituciones o cómo una población pasa de un estado a otro, no dan cuenta de los individuos y las relaciones, sino que los dan por supuestos (esto se explicita al definir el juego). Ahora bien, las reglas del juego y las características de los individuos y la sociedad pueden verse como equilibrios de juegos subyacentes (no necesariamente juegos evolutivos, pero sí juegos o mecanismos de nivel inferior).

Un punto importante a favor de la propuesta es que los juegos evolutivos permiten explicar cómo la sociedad puede llegar a estados no planeados ni deseados. Es decir, permiten explicar las consecuencias no intencionales de la interacción. Este tipo de consecuencias no planeadas son difíciles de explicar (dado que se requerirían grandes concatenaciones) apelando solo a los tres tipos de mecanismos propuestos por Hedström y Swedberg (1996, 1998b) y comentados en el capítulo 4, §2: mecanismos macro-micro, micro-micro y micro-macro.

En suma, la teoría de juegos evolutivos podría ser una herramienta adecuada para modelar mecanismos macro-macro. Y esos mecanismos no necesariamente tienen que ser sociales: pueden ser meramente conductuales, sin que esa conducta suponga racionalidad. De hecho, Gintis (2007)^[48] propone que la teoría de juegos evolutivos puede ser el lenguaje formal que permita un tratamiento común de ciertas áreas de solapamiento entre las ciencias conductuales. Dos diferencias importantes distinguen la propuesta de Gintis de la propuesta que aquí se está planteando: en primer lugar, Gintis no habla de mecanismos; en segundo lugar, aquí no se propone que la teoría de juegos evolutivos sea el lenguaje formal común a distintas disciplinas, sino que son los mecanismos los que permiten la interdisciplinariedad, y la teoría de juegos evolutivos puede ser una de las herramientas empleadas para modelar mecanismos.

Cowen (1998) discute algunos problemas de la teoría de juegos para modelar mecanismos sociales, particularmente el problema de las indeterminaciones generadas por los múltiples equilibrios. Se refiere a los juegos clásicos, no evolutivos ni cíclicos, en los cuales puede hablarse de modelación de mecanismos micro-macro. Menciona, al pasar, que tal vez los juegos evolutivos puedan dar una respuesta. Mayntz (2004, pp. 255–256) sostiene que los mecanismos sociales no pueden ser capturados por la teoría de juegos, porque los mecanismos sociales involucran “una constelación” de jugadores, y una constelación de jugadores no es modelable. Esto es correcto para los juegos clásicos, que en su forma normal o extensiva suelen incorporar pocos jugadores (usualmente dos o tres), pero no para los juegos evolutivos como el que se ha mostrado aquí, en los cuales el número de jugadores no está limitado.

3. Guía de la investigación

Una tercera ventaja del enfoque neomecanicista, señalada en distintos campos es que los mecanismos pueden guiar la investigación. Mahoney (2003), por ejemplo, sostiene que los mecanismos causales pueden ayudar en la investigación derivando proposiciones empíricamente evaluables. En la misma línea, está Hernes (1998, p. 78), quien sostiene que hay una lógica de la investigación (recuérdese que Hernes considera los mecanismos como constructos analíticos): (1) comienza con una observación, (2) se provee una lista de modelos candidatos para la explicación, (3) se derivan implicaciones de esos modelos, (4) se evalúa la evidencia (se evalúan las implicaciones con los datos disponibles), y (5) se eliminan aquellas explicaciones que no estén debidamente respaldadas por los datos (Cf. Stinchcombe, 1968). En general, la idea de quienes conciben los mecanismos como constructos analíticos es que esos constructos deben ser evaluados. En muchos casos (tanto en ciencias naturales como sociales) los modelos guiarán el diseño de los experimentos. Y una parte importante de la investigación será “ascender” en generalidad: si se modela sobre un caso o unos pocos casos, robustecer el modelo implica ir descubriendo otros mecanismos (concretos) que ese modelo captura. Tilly (2001b) sostiene que el adoptar las explicaciones mecanicistas tiene fuertes implicaciones en la investigación y análisis de las ciencias políticas. Por ejemplo, reorientar las explicaciones de la mera narrativa sobre episodios a la búsqueda de procesos. Esto es, ante un episodio que puede describirse, abstraer las características salientes y buscar otros episodios con las mismas características. O la comparación de los mecanismos y procesos. O la integración de los tres tipos de mecanismos que reconoce: cognitivos, relacionales y ambientales. Al conceptualizar sobre mecanismos, se los concibe aisladamente, pero en la realidad se dan en interacción.

Estas propuestas que se acaban de comentar no difieren tanto de otras, particularmente de la que pone la búsqueda de leyes como centro de la tarea científica^[49].

Mucho más distintiva es la propuesta de Bechtel y Abrahamsen (2005): los mecanismos proveen herramientas para identificar y descubrir^[50] mecanismos. El científico debe identificar las unidades del mecanismo y determinar las propiedades y relaciones y entender cómo están organizadas para generar el fenómeno. Esto requiere separar el mecanismo, ya sea física o conceptualmente. Bechtel y Richardson (1993) han llamado a este proceso descomposición (decomposition). Hay dos formas de descomposición, que pueden llevarse a cabo simultáneamente o por separado: estructural y funcional. En la descomposición funcional, la estrategia es comenzar con el funcionamiento (o conducta) global del mecanismo y luego calcular qué operaciones de nivel inferior contribuyen para lograrlo (o lograrla). En los términos propuestos aquí en el capítulo 3, la estrategia consiste en indagar los cambios en las propiedades y relaciones de las unidades (es decir, en las resultantes de relación) para ver si algunos de esos cambios son causados por mecanismos de nivel inferior. Es decir, buscar si hay mecanismos de nivel inferior que cumplen cierta función en el mecanismo (conocido) de nivel superior.

Bechtel y Abrahamsen (2005) dan un ejemplo de descomposición funcional: el sistema bioquímico que ejecuta el metabolismo en las células, por ejemplo, cataboliza la glucosa en dióxido de carbono y agua. Las operaciones componentes son caracterizadas en términos de reacciones químicas individuales en una serie de sustratos (por ejemplo, oxidarlos, reducirlos o agregarles H2O). Una descomposición funcional exitosa de este sistema identificará cada operación y sus partes pasivas (el sustrato y el producto resultante). Falta la especificación de las partes activas, es decir, de la enzima que inicia y guía la reacción. Una vez que las partes están identificadas, una descomposición estructural acompaña la descomposición funcional.

La descomposición estructural es la búsqueda de “las partes actuantes” (working parts), es decir, los componentes estructurales que ejecutan las operaciones que figuran en la descomposición funcional. Un ejemplo de descomposición estructural: la investigación citológica sobre las organelas de la célula.

El objetivo último de la investigación es unir las operaciones con las partes. A esto se llama localización. Por ejemplo, se pueden diferenciar tres operaciones principales en la respiración celular: glicolisis en el citoplasma, ciclo del ácido cítrico en la matriz de la mitocondria, y las operaciones asociadas de transporte de electrones y fosforilación oxidativa en las crestas.

La habilidad para relacionar partes con operaciones proporciona un medio para corroborar cada descomposición: relacionar una operación componente con una parte componente (esto es, según los términos empleados aquí en el capítulo 3, relacionar una propiedad o relación con algunas unidades de análisis) identificada independientemente provee evidencia de que ambos figuran realmente en el mecanismo. Por el contrario, el fallo en relacionar partes con operaciones da motivos para dudar de la existencia ya sea de la parte, ya sea de la operación.

La tarea de descomposición puede involucrar una variedad de procedimientos experimentales, que incluyen la inhibición de un componente para observar su efecto en el funcionamiento global o el registro de las condiciones internas del mecanismo mientras opera bajo diferentes condiciones.

Según Bechtel y Abrahamsen (2005) los desafíos para testear hipótesis son los mismos para mecanismos y para leyes. Quien testea mecanismos hipotetiza cómo el mecanismo o sus componentes se comportarán bajo determinadas condiciones y usará los resultados de someter de hecho el mecanismo a esas condiciones para evaluar el mecanismo propuesto (al menos, cuando sea posible). En principio, los mismos desafíos enfrenta el evaluar mecanismos y el evaluar leyes. Pero testear mecanismos tiene una ventaja: es más probativo que testear leyes. Esto es porque generalmente la evaluación se centra en elementos específicos del mecanismo y no en el mecanismo como un todo. Por esto, cuando la expectativa falla, el resultado usualmente tiene la fuerza de un diagnóstico: muestra cómo los componentes hipotetizados difieren de los componentes reales. Los resultados señalan directamente las revisiones necesarias. Entonces, los resultados sobre el testeo de mecanismos son frecuentemente mucho más informativos que los de las leyes.

La investigación en mecanismos es mucho más que proponer hipótesis y testearlas. La investigación típicamente comienza con una descripción sobresimplificada en la cual solo se especifican unos pocos componentes y aspectos de la organización del mecanismo. Con el tiempo, se la revisa y completa repetidamente.

El resultado se parece mucho más a un programa de investigación (Lakatos, 1970) que a la descripción clásica de testeo de teorías (Bechtel y Abrahamsen, 2005, p. 437).

4. Causalidad

Torres (2009) señala, además de la relevancia explicativa, que los mecanismos podrían resolver el problema de la causación, al formular explicaciones reduccionistas de la causación en términos puramente mecanicistas. Esta idea del reduccionismo y la causalidad también está presente en toda la literatura neomecanicista, independientemente de qué disciplina se trate^[51].

Claramente, los mecanismos (como se los ha entendido desde el primer momento en este trabajo) son causales. El mecanismo es causante de una conducta: un cambio en el sistema, que pasa de un estado inicial a un estado final. La idea según la cual los mecanismos pueden ser una respuesta al problema de la causalidad planteado por Hume es clara. De todas maneras, como ya se ha dicho, aquí se considera que no todo fenómeno es causado por mecanismos. Es por esto que, dejando de lado la discusión sobre si todo fenómeno tiene una causa, es claro que no todo fenómeno puede ser causalmente explicado apelando a mecanismos. Además, para que los mecanismos den una respuesta satisfactoria al problema de la causalidad, deben estar correctamente identificados y ser deterministas. Y no todos los mecanismos son deterministas. Además, hay mecanismos cuyas condiciones detonantes no son del todo conocidas (no se sabe cuándo se accionarán, como el caso del mecanismo causante del cáncer o la úlcera de duodeno desarrollado en el capítulo 2, §7). Que los mecanismos produzcan cambios regulares no significa que solucionen el problema de la causalidad, pero sí puede sostenerse que, cuando se tiene un mecanismo debidamente identificado y testeado, se tiene una buena solución al problema de la causalidad: se sabe qué es lo que produce el cambio y cómo lo hace.

De la misma manera que el problema de la causalidad es tratado en términos de contrafácticos, se ha tratado de llevar los contrafácticos al plano de los mecanismos para caracterizar la producción regular de cambios de la cual ellos son responsables: Glennan (2002) retoma el tratamiento de los contrafácticos que hace Woodward (2000), y Woodward (2002) toma los mecanismos tal y como los define Machamer, Darden y Craver (2000) para discutirlos en términos de contrafácticos. Psillos (2004) propone que mecanismos y contrafácticos deben trabajar en tándem para poder tener un buen tratamiento de la causalidad.

En todo caso, la construcción de modelos que describen mecanismos causales presenta una diferencia crucial con la búsqueda de leyes causales: la actitud ante los contraejemplos. Los modelos tratan de capturar situaciones reales observadas. Esa modelación es una idealización y requiere, necesariamente, abstracción. Si el modelo parece adecuarse al mecanismo, lo que sigue es buscar otros mecanismos similares. Así el modelo gana en generalidad y robustez. Y si el modelo no describe adecuadamente un determinado mecanismo, podrá describir adecuadamente otros. Y si no es aplicable a algunos, podrá aplicarse a otros. El punto es que no puede hablarse de “contraejemplos” o “refutaciones”. Los modelos serán o no adecuados, pero no serán “falsos”. Con la búsqueda de leyes causales pasa algo totalmente distinto. Una ley causal entra en estado de duda ante casos que no se adecúan a lo que la ley describe. Puede investigarse qué condiciones necesarias fallan, pero la ley como tal entra en estado de duda. En el caso más extremo, la ley será considerada falsa o refutada por la experiencia.

Como se dijo en el capítulo 3, §3, una de las propuestas más difundidas y analizadas de caracterización de los mecanismos es la concepción dualista (según la cual, los mecanismos constan de partes y actividades). Uno de los problemas de la propuesta dualista es que no todas las actividades que ejecutan las entidades son causalmente relevantes, con lo cual parece haber un problema para determinar cuándo una actividad es productiva (o causalmente relevante para la operación del mecanismo). En los términos de la caracterización propuesta aquí, el problema es identificar correctamente las resultantes de relación relevantes al funcionamiento del mecanismo. Bogen (2008a) propone y discute una respuesta a la pregunta sobre qué distingue una coocurrencia causal de una no causal. La respuesta deriva de la idea de Elizabeth Anscombe de que la causalidad es un concepto altamente abstracto cuyo significado deriva de nuestro entendimiento de actividades causalmente productivas específicas (como tirar o quemar) y de su rechazo del supuesto de que la causalidad puede ser informativamente entendida en términos de regularidades contrafácticas o de hecho. Si bien los términos del análisis de Bogen son los de la concepción dualista, el análisis puede aplicarse perfectamente a la caracterización de mecanismo propuesta aquí en el capítulo 3, dado que lo dicho sobre partes y actividades vale para también para unidades de análisis, relaciones, propiedades y resultantes de relación^[52].

Anscombe (1981) rechaza las teorías que tratan de reducir la noción de causalidad a las nociones de regularidad, entre ellas, la de Hume. Sostiene que la causalidad es una cosa y la regularidad otra, aunque reconoce que las causas que operan regularmente son de mayor interés teórico y práctico. Anscombe también rechaza la idea de que la causa implica necesidad (to cause is to necessitate): la idea de causa no implica que, dada la causa, sea imposible que el efecto no ocurra (es decir, siempre parece posible encontrar alguna forma de impedir el efecto vía interferencia).

Anscombe afirma que no se puede explicar qué significa que una cosa cause otra sin recurrir a conceptos que son en sí mismos irreductiblemente causales^[53]. Es decir, conceptos causales generales como rayar, empujar, mojar, llevar, comer, quemar, derribar, hacer –ruidos, barquitos de papel–, y otros similares, son apoderados –o marcadores de posición– (placeholders) que derivan su significado a partir de conceptos causales específicos. Si –agrega Bogen (2008a, p. 113)– entendemos palabras que significan rayar, aplastar, y demás, podemos entender términos generales como causa.

Hay un ejemplo muy conocido contra la explicación causal presentada por Hempel (el submodelo de la explicación nomológico deductiva), que puede encontrarse en Salmon (1971, p. 34). El razonamiento es:

(Ley:) Todo hombre que regularmente toma pastillas anticonceptivas evita quedar embarazado. (Condición inicial:) John Jones ha tomado regularmente las pastillas anticonceptivas de su esposa. Ergo, John Jones evitó quedar embarazado.

Según Salmon, la deducción en este razonamiento es válida, pero no es explicativa.

Según Bogen, ante este ejemplo Anscombe recurriría a un hecho empírico: en el cuerpo masculino los químicos que contienen las pastillas anticonceptivas que tomó John Jones no pueden ejercer las acciones que previenen el embarazo. Usualmente, los anticonceptivos vía oral incluyen diferentes químicos, cada uno de los cuales se interpone en distintos sistemas: un químico suprime las hormonas necesarias para que el ovario libere óvulos; otro actúa en la mucosa cervical (la mucosa del cuello uterino) engrosándola para que el esperma no pueda moverse a través de ella; otro actúa en el revestimiento del útero para hacerlo no apto para la implantación del óvulo fecundado; otro actúa como espermicida. La razón por la cual las pastillas no previenen el embarazo en los hombres es que los hombres no tienen ovarios o útero en los cuales actúen los químicos, ni óvulos a ser fertilizados por el esperma.

Entonces, los hombres no quedan embarazados porque el aparato reproductor masculino está compuesto de partes que no pueden engranar en las actividades causalmente productivas en las que deberían para producir el embarazo. En otras palabras, los sistemas son distintos en hombre y mujeres, y para que opere un mecanismo anticonceptivo (esto es, para suprimir hormonas, engrosar la mucosa cervical, etc.) se requieren unidades que solamente están presentes en las mujeres. Por lo tanto, el “mecanismo anticonceptivo” que opera en las mujeres (cuando ingieren las pastillas anticonceptivas) no puede ser el mismo que opera en los hombres.

Los químicos de las pastillas engranan en algunas actividades causalmente productivas en el hombre que las toma; de hecho, las pastillas se disuelven en el estómago y los químicos son asimilados. ¿Por qué no causan la prevención del embarazo? Woodward (2004) trata el mismo ejemplo, y propone que la respuesta a esta pregunta depende del hecho de que la no-preñez en machos no depende contrafácticamente de las actividades en que engranan los químicos del control de la natalidad cuando los machos los ingieren. Por el contrario, hay una dependencia contrafáctica entre la no-preñez en las mujeres y las actividades en que engranan los químicos que ingieren. En ambos casos, se obtiene la dependencia relevante solo si la no-preñez habría resultado en versiones idealizadas de John y su fértil esposa Joan si hubieran tenido lugar intervenciones ideales para promover o amortiguar las actividades de los químicos en sus cuerpos.

La respuesta anscombiana, sugiere Bogen, recurriría no a los contrafácticos, sino a los hechos sobre los químicos y las actividades causalmente productivas en las cuales ellos engranan. Si sabemos lo suficiente sobre los químicos en cuestión y sus actividades como para poder derivar conclusiones contrafácticas sobre lo que resultaría de una intervención sobre ellos, como propone Woodward, entonces podremos implementar la respuesta anscombiana sin necesidad de esos contrafácticos. Si se sabe que Jones no tiene útero, ovarios y óvulos, no es necesario recurrir a contrafácticos para explicar por qué los químicos que suprimen las hormonas, engrosan la mucosa cervical y matan el esperma no son los responsables por su no-preñez.

Bogen sostiene que, según Anscombe^[54], es un hecho en bruto (brute fact) que, por ejemplo, la actividad de tirar de una puerta puede abrirla, más que acompañar coincidentemente la apertura de la puerta o que rayar una zanahoria remueve (en lugar de acompañar coincidentemente la remoción de) la piel. Si tiene razón, es equivocado buscar un una descripción general de la causalidad como lo intentan Hume, Hempel o Woodward para explicar por qué ninguna actividad causalmente productiva específica es relevante para la producción de un efecto. En lugar de sugerir una respuesta general y uniformemente aplicable a la pregunta sobre lo que diferencia las causas de las no-causas, Anscombe (así lo interpreta Bogen) propone un tratamiento gradual de preguntas sobre cómo se producen efectos específicos. Según esta perspectiva, que un factor dado haga una contribución causal para la producción de un efecto dado depende de hechos contingentes, empíricamente comprobables, sobre cómo se comportan las cosas relevantes y qué resulta de su conducta.

Cabría, según Bogen, hacer dos preguntas a la postura anscombiana: la primera pregunta apunta a las cosas que se pueden percibir. La concepción humeana de causalidad se basa en la regularidad de percepciones, es decir, depende de la percepción. De igual manera, puede preguntarse si las actividades causalmente productivas son algo perceptible, en otras palabras, si la concepción anscombiana es psicológicamente realista. La segunda pregunta se refiere al concepto de actividad causalmente productiva. Más específicamente, la pregunta sería si actividad causalmente productiva es un concepto unificado o una generalidad arbitraria.

Con respecto a la primera pregunta, Bogen analiza algunos trabajos sobre la percepción, particularmente sobre la percepción relacionada a la causalidad. La gramática, apunta Bogen, es un ejemplo de algo que puede ser pensado sin ser percibido, es decir, sin ser reducible a algo que pueda verse, leerse u oírse. De la misma manera, no es necesario creer que la causalidad o las conexiones causales son perceptibles para creer que tenemos conceptos de actividades causalmente productivas. El equipo de Alison Gopnik ha hecho experimentos que aportan evidencia contra la postura de Hume: niños muy pequeños tienen razonamientos causales y adquieren conceptos causales que van más allá de las generalizaciones de coocurrencias o regularidades observadas. Los estudios de Gopnik y Schulz (2004), y Harris, German y Mills (1996) muestran que las ideas de Anscombe son psicológicamente adecuadas, dado que los niños pueden establecer razonamientos causales que emplean conceptos de actividades causalmente productivas. En este sentido, también sería psicológicamente adecuada la propuesta sobre actividades causalmente productivas o resultantes de relación.

Con respecto a la segunda pregunta, lo que importa es cómo definir o caracterizar el término actividad causalmente productiva.

Beckner (1968, p. 22) distingue entre conceptos monotípicos (monotypic) y conceptos politípicos (politypic). Un concepto es monotípico cuando la posesión de una propiedad no disyuntiva es una condición suficiente y necesaria para que algo caiga bajo el concepto^[55]. Por ejemplo, la propiedad de ser una figura cerrada, plana y limitada por tres líneas rectas es condición necesaria y suficiente para que algo califique como triángulo. El concepto de reyezuelo de corona roja (Regulus calendula; en inglés ruby crowned kinglet), por ejemplo, es, por el contrario, un concepto politípico^[56]. Esto significa que existe una colección G de propiedades, tal que cada reyezuelo de corona roja posee un gran (pero no especificado) número de propiedades en G, y cada propiedad en G es poseída por un gran número de aves, y ninguna propiedad de G es poseída por cada individuo de la colección. Este último requisito elimina de G las propiedades que pueden ser trivialmente atribuidas a todo.

Según Bogen, las actividades causalmente productivas no son politípicas en el sentido de Beckner, porque no hay un G cuyos miembros sean propiedades no disyuntivas poseídas en gran número por cada caso concreto de actividad causalmente productiva (como empujar, comer o despolarizar). Por el contrario, las actividades causalmente productivas son demasiado diversas como para encontrar un G tal que cada uno de sus miembros sea poseído por un gran número de actividades causalmente productivas.

Para Bogen, la concepción aristotélica captura mejor que la beckeriana el concepto de actividad causalmente productiva. Según Aristóteles, algunos conceptos (perfectamente útiles e inteligibles) no pueden ser capturados por las definiciones que brindan condiciones suficientes y necesarias, y deben más bien ser explicados por medio de analogías: el que ve y el que tiene los ojos cerrados están en la misma relación que el producto terminado y el material en bruto (es decir, el primero está en acto respecto de lo que el segundo está en potencia). Entender tales conceptos (como estar en acto y estar en potencia) es captar las conexiones que establecen las analogías. Lo que tienen en común las diferentes actividades que caen bajo el concepto de actividad causalmente productiva es que: cada una es similar o análoga a otra(s) con respecto a las características que son causalmente relevantes en la producción de sus efectos^[57]. No es necesario que las similitudes y analogías sean las mismas para un gran número de actividades causalmente productivas. Las características con respecto a las cuales valen estas analogías deben ser “causalmente relevantes”, pero si no existe un criterio universalmente aplicable para distinguir las causas de los factores que coocurren, no habrá tampoco un criterio único, universalmente aplicable para la relevancia causal. La investigación científica requiere que se reconozcan las resultantes de relación, así se podrá tener una comprensión de los procesos causales de los cuales son responsables los mecanismos. Lo esencial para Bogen es la productividad de los mecanismos, es decir, la propiedad de provocar cambios. Y los elementos últimos, los que permiten entender el concepto de causalidad, son las actividades, esto es, las resultantes de relación responsables de los cambios que típicamente produce un mecanismo.

Los filósofos que buscan una condición única, universalmente aplicable, libre de excepciones (tal como “las causas necesariamente dan lugar a los efectos”, “los efectos dependen contrafácticamente de sus causas”, “causas y efectos son casos particulares de regularidades legaliformes”) para discriminar causas de factores no causales que acompañan la producción de un efecto no estarán, evidentemente, satisfechos con la posición anscombiana desarrollada por Bogen. De todas maneras, puede sostenerse que lo relevante para el enfoque neomecanicista –al menos para la investigación científica– no es encontrar un criterio o condición definitoria de causa (o de actividad causalmente relevante), sino más bien encontrar para cada caso, cuáles son las actividades (relaciones y propiedades) que intervienen en la operación de un mecanismo. Una manera (no la única) de determinar cuáles son las actividades relevantes es la intervención: la manipulación de factores para interrumpir la operación de los mecanismos. Y encontrar las actividades en los mecanismos es, finalmente, encontrar las causas (Machamer, 2004, pp. 27–28).

La propuesta neomecanicista del tratamiento de la causalidad no busca leyes causales ni se apoya en los contrafácticos. Identificar un mecanismo tal como se lo concibe aquí implica identificar cómo es que el cambio se produce, y eso se logra cuando se han identificado las resultantes de propiedades y relaciones. Y esta identificación depende, como toda identificación de una contribución causal en la propuesta anscombiana, de hechos contingentes, empíricamente comprobados, sobre cómo se comportan las unidades, y qué resulta de su conducta. Es a partir de la comprensión de estos fenómenos empíricos como se logra ganar entendimiento respecto de conceptos generales como el de causalidad. De todas maneras, y como ya se ha señalado con respecto a otros aspectos del neomecanicismo, la propuesta de análisis causal no necesariamente debe verse como alternativa (para proponerse como tal, debería compararse con las demás posturas). La propuesta neomecanicista puede verse, una vez más, como complementaria de otras propuestas (Psillos, 2004).

5. Etcétera

Distintos autores señalan otras ventajas del enfoque basado en mecanismos, ventajas que por una cuestión de espacio solo serán mencionadas aquí. Por ejemplo, los mecanismos serían una alternativa al reduccionismo o permitirían un análisis de las propuestas reduccionistas. Craver (2005) propone que la integración de los distintos niveles en neurociencia debe darse en términos de mecanismos, en lugar de integrarlos por medio del reduccionismo. Darden (2005) analiza la relación entre la genética mendeliana y la biología molecular, relación que ha sido planteada como reduccionismo. La autora muestra cómo el enfoque mecanicista permite un mejor análisis del reduccionismo, y propone una alternativa. Según Darden, cada disciplina estudia mecanismos distintos, aunque fuertemente conectados: los mecanismos hereditarios tienen diferentes entidades y operan en diferentes momentos en una sucesión temporal de mecanismos hereditarios.

En ciencias sociales, la estrategia reduccionista de abrir las cajas negras y buscar lo que relaciona las variables está en el corazón mismo de la propuesta (Hedström y Swedberg, 1998b). Ese “abrir las cajas negras” consiste en tratar de reducir los resultados en lo social recurriendo a ciertos rasgos de la conducta individual. Abbot (2007a, 2007b) discute con Baldassarri (2007), Manzo (2007) y Vitale (2007) la relación entre el enfoque mecanicista y el relacionista. En principio, la propuesta de Abbot difiere de la propuesta mecanicista, pero el mismo autor termina admitiendo que su propuesta relacionista se ha vuelto, con el tiempo, mecanicista y que el programa mecanicista ha resultado más exitoso que el propio^[58].

En biología, Craver y Darden (2005, p. 234) mencionan el éxito de las explicaciones que recurren a mecanismos en biología como exitosas frente a diferentes formas de vitalismo y a explicaciones que apelan al diseño inteligente.

Baker (2005) construye (véase capítulo 4, §7) una nueva taxonomía de la especiación basada en los mecanismos subyacentes. Esto muestra que poner los mecanismos en un lugar central de la investigación y la teorización puede llevar a nuevas clasificaciones, mejores y más fructíferas. Algo parecido se comentó en este capítulo (§1.2): Brante (2008) es quien propone que las taxonomías por sí solas son insuficientes, que requieren justificación y que los mecanismos pueden dar esa justificación de por qué las cosas son como son.

Barros (2008) sostiene que los mecanismos deterministas permiten predicciones confiables (a menos que haya interferencia), y que los mecanismos estocásticos (como los involucrados en la selección natural) permiten predicciones solo si la probabilidad es mayor al 50% (aunque estas predicciones son menos confiables). Esto es, los mecanismos pueden ser útiles para la predicción de fenómenos.

Craver (2001) propone que los mecanismos pueden brindar un análisis funcional adecuado. Toma el análisis de Cummins (1975) y lo sintetiza con el concepto de mecanismo para capturar el sentido de función en biología. Uno de los objetivos que se propone es el de integrar los distintos nivele jerárquicos: aislado (o, por llamarlo de alguna manera, “de nivel 0”), contextual (“de nivel 1”) y constitutivo (“de nivel –1”). El análisis de la función en el mecanismo permitiría un tercer tipo de explicación causal (además de las definidas por Salmon, 1984: etiológica y constitutiva): la explicación contextual.

Craver y Alexandrova (2008) proponen que la economía y la neurociencia pueden integrarse en neuroeconomía bajo la metodología propuesta por el neomecanicismo. La neuroeconomía es caracterizada como el intento de descubrir los mecanismos neurales en virtud de los cuales las personas calculan, por ejemplo, recompensas, consecuencias u opciones, y tiene como objetivo explicar las regularidades en la toma de decisiones, específicamente en la conducta económica. Una nueva perspectiva, como la neuroeconomía puede provocar –según la concepción kuhniana del progreso científico– una revolución: la nueva concepción es adoptada, y las anteriores abandonadas. La propuesta de Craver y Alexandrova es que, si se adopta el enfoque neomecanicista, no será necesaria ninguna revolución y sostienen que la economía y la neurociencia podrán integrarse porque, por una parte, el resto de las neurociencias, la biológica y la cognitiva, han adoptado y mantienen el enfoque neomecanicista,^[59] y por otra, los objetivos de la economía, como la predicción, la explicación y el control, son compatibles con el enfoque neomecanicista y pueden lograrse identificando debidamente los mecanismos.

Kittel (2006) discute la observabilidad de los mecanismos sociales. En este campo, la búsqueda de mecanismos (sean o no observables) puede plantearse como un “puente” entre la metodología cuantitativa y la cualitativa. La propuesta, grosso modo, es que a la investigación cualitativa la identificación de los mecanismos le permitiría ganar generalidad, mientras que a la investigación cuantitativa le permitiría ganar en comprensión y en poder explicativo.

Schelling (1998) sostiene que una de las ventajas de comprender los mecanismos sociales que subyacen a las regularidades de comportamiento es la posibilidad de intervención: por ejemplo, a través de la publicidad.

Stinchcombe (1991; 1998) sostiene que los mecanismos pueden colaborar con la teoría, haciéndola más flexible, más exacta o más elegante. De hecho, sostiene (recuérdese que se ha dicho que Stinchcombe da una caracterización de índole epistémica) que los mecanismos son útiles a las teorías en tanto les brinden alguna de esas características.

Erik Weber (2007, 2008)^[60] sostiene que los mecanismos sociales son realmente útiles y hasta necesarios en ciencias sociales, no para brindar la comprensión causal, sino para establecer la relevancia política de las afirmaciones causales. En ciencias sociales los experimentos son, por cuestiones éticas, rara vez factibles. Cuando puede experimentarse, las condiciones son usualmente tan irreales para los sujetos que difícilmente sea válida una extrapolación de los resultados “al mundo real”. Cuando no puede experimentarse y se trabaja con modelos de simulación, ocurre algo similar. Incluso con estudios de campo prospectivos y retrospectivos se tiene el problema de la extrapolación: por cuestiones presupuestarias estos estudios usualmente se limitan a pocos sujetos de un ámbito acotado, con lo cual los resultados difícilmente puedan generalizarse a otros sujetos y otros ámbitos. Los mecanismos –sostiene Weber– son entonces la manera que tienen (y, de hecho, usan) los científicos para llevar a cabo esas extrapolaciones.

---