De la capa física a la lógica
Es posible que surja una pregunta: si programar implica construir software, ¿por qué comenzar hablando de los componentes físicos de la computadora? ¿No es el software completamente lógico? Para entender esta conexión, es importante reflexionar sobre cómo el álgebra de Boole permitió que se construyera el hardware de las computadoras.
El álgebra de Boole es un sistema matemático que trabaja con valores de verdadero o falso (a veces representados como 1 o 0), y estas operaciones matemáticas son la base de la lógica en las computadoras.
Esta lógica booleana fue crucial para el desarrollo de los circuitos electrónicos en las computadoras, ya que los transistores y otros componentes electrónicos funcionan con valores binarios, encendido (1) o apagado (0), que representan las decisiones lógicas básicas.
¿Cómo se conecta todo esto?
Los componentes físicos de una computadora, como los transistores, son interruptores electrónicos que pueden estar en uno de dos estados: encendido (1) o apagado (0). Estos transistores, trabajando en conjunto, permiten realizar operaciones lógicas básicas, como las de AND, OR y NOT, que son fundamentales en el álgebra de Boole. Por ejemplo, un puerto AND en un circuito electrónico solo deja pasar una señal (o produce un “1”) si ambas entradas son “1”. Esto es exactamente lo mismo que la operación lógica AND que aprendes en álgebra de Boole. De manera similar, un puerto OR produce un “1” si al menos una de sus entradas es “1”, y esto refleja la lógica OR.
Lógica humana versus lógica booleana
Es importante diferenciar entre lo que pensamos y lo que está grabado en el hardware de las computadoras. Mientras que la lógica booleana es un sistema muy adecuado para la electrónica y la programación, nosotros, como seres humanos, no pensamos estrictamente en base a la lógica booleana.
En nuestra forma natural de pensar, usamos una lógica más pragmática y flexible, que se adapta a situaciones cotidianas y contextuales. Esto significa que no siempre seguimos las reglas de la lógica booleana de manera estricta como lo haría una computadora.
Aunque los circuitos electrónicos de las computadoras operan bajo principios lógicos exactos, basados en el álgebra de Boole, esto no implica que nuestra manera de pensar funcione de la misma forma. Es decir, aunque los programas y sistemas informáticos están construidos con lógica booleana, nuestra mente opera con un tipo de razonamiento mucho más complejo y menos rígido, que no entra en los estrictos límites de la lógica formal.
La lógica tiene una materialización en el hardware.
Es importante entender que la lógica de las computadoras no es algo que ocurre en el cerebro humano o en un nivel abstracto. Esta lógica tiene una materialización física en los componentes electrónicos. Es decir, cuando programamos, estamos interactuando con una máquina que está tomando decisiones basadas en reglas lógicas, pero esas decisiones no son solo abstractas: dependen de caminos físicos en los circuitos, que se activan o desactivan en función de los valores lógicos.
Por eso, cuando comenzamos a estudiar programación, es fundamental entender que la lógica que utilizamos en el software tiene una conexión directa con los circuitos electrónicos que la implementan físicamente.
Los programas que escribimos no solo existen como ideas o instrucciones abstractas, sino que también están siendo ejecutados por hardware que realiza esas operaciones lógicas de manera muy real y tangible. Es por eso por lo que comenzamos hablando de la capa física, los componentes electrónicos. Sin ella, no sería posible ejecutar la lógica de los programas. A medida que avanzamos hacia la programación, agregamos capas de abstracción sobre esa lógica física, y las abstracciones están dirigidas a objetivos que se plantean en el mundo real en el cual se deben automatizar las tareas. Pero siempre debemos recordar que todo lo que ocurre en el software tiene un fundamento en los circuitos que físicamente ejecutan esas instrucciones lógicas.
Lógica y argumentación como complementos.
En las carreras relacionadas con las CC, se comienza a utilizar la lógica formal proposicional en las primeras asignaturas de programación. Esto se debe a que las proposiciones lógicas son fundamentales para tomar decisiones dentro de un programa, como las bifurcaciones (si… entonces) y las repeticiones (mientras…).
Por lo general, se aprenden los conceptos básicos de lógica proposicional en asignaturas como Matemática Discreta o Lógica I, que suelen dictarse de manera simultánea o con anterioridad a las clases de programación, dependiendo de cómo esté organizada la carrera.
Investigaciones en psicología y ciencias cognitivas han demostrado que no siempre se utiliza la lógica formal de manera natural en la vida cotidiana. En realidad, la forma en que las personas razonan suele estar más relacionada con el contexto o con lo que les resulta más práctico en ese momento, en lugar de seguir reglas lógicas estrictas.
Este hallazgo es especialmente importante cuando se aplica la lógica a la programación. Aunque se conozcan las reglas lógicas formales, pueden aparecer dificultades para relacionarlas correctamente con los problemas en el mundo real que debe resolver un programa. Por eso, es importante aprender a aplicar la lógica en situaciones conocidas, donde se observe cómo efectivamente se utiliza .
A continuación, se propone una actividad que le ayudará a los estudiantes a modelar esas reglas en contexto.
Actividad: El problema irresoluble
Te invitamos a analizar dos problemas de toma de decisiones en los que debes desentrañar las condiciones lógicas subyacentes.
Las situaciones del mundo real a menudo ocultan relaciones que pueden ser aclaradas a través de un modelo lógico. La práctica se basa en el episodio “The Movie Theatre Conundrum” de la serie “The Big Bang Theory” y completar los ejercicios propuestos a partir de él.
Sheldon y sus amigos no logran resolver un problema. Planean ver una película en el cine luego de cenar. Pueden elegir entre varios cines en la ciudad y varios restaurants.
Sin embargo, las pretensiones de Sheldon son demasiado exigentes comparadas con las de sus amigos. Para que un cine y un restaurant sean aprobados por Sheldon, deben cumplir estrictamente con determinadas condiciones. El cine debe vender regaliz negro y tener máquinas de granizado. El restaurant debe estar cerca del cine para cenar antes de ver la película.
Sus amigos intentan convencerlo de opciones más flexibles, como aceptar la ausencia de máquinas de granizado a cambio de batidos o valorar los asientos reclinables, por ejemplo. Pero Sheldon no tolera que no se cumplan cada una de las condiciones establecidas.

Deben cumplirse A y B y C
Leonard piensa que los cines tachados son aceptables porque tienen proyección digital y sonido surround (envolvente).
Según Rajesh, uno de los cines es aceptable porque se trata de un multicine, y los asientos son cómodos. Pero Sheldon advierte que en ese cine no tienen regaliz negro sino rojo, y esa golosina le sienta mal.
Rajesh propone cenar después del cine. Pero Sheldon dice que no es posible porque retrasaría su digestión.
Ejercicio 1
En el enunciado anterior las variables y los valores posibles están resaltados en itálica. Distingue cuáles son variables y cuáles valores. ¿Qué otras variables/valores podrías identificar?
El problema está planteado por un grupo de personas, cada una de las cuales aporta un conjunto de condiciones para realizar la acción que podrá ser más restrictivo o flexible dependiendo, en este caso, del carácter de los personajes.
Ir al cine los cuatro juntos implica que todos deben estar de acuerdo con el elegir el cine, esto es, que el cine debe ser aprobado por los cuatro.

La condición conjunta es más exigente que la simple disyuntiva. En general, es más difícil que suceda p y también q y también r, a que suceda uno cualquiera de los tres.
Ejercicio 2:
Escribe un ejemplo de situación cotidiana donde se utilice una conjunción.
Las condiciones se expresan mediante proposiciones, a veces llamadas premisas o conclusiones dependiendo de su rol en el argumento. Desde la vida cotidiana hasta la lógica formal hay niveles de abstracción: las proposiciones expresadas en el lenguaje cotidiano son simples afirmaciones sobre las cosas.
En un lenguaje artificial como el pseudocódigo, se parecen a un programa. Las condiciones expresadas en pseudocódigo utilizan palabras. Esto es, también se asemejan al lenguaje humano, ya que los lenguajes artificiales han evolucionado hacia un formato natural. Y en un lenguaje totalmente abstracto como la lógica formal, se expresan de un modo más sintético.
Para volcar estas condiciones en una tabla de verdad, sintetizamos la forma de expresarlas: en vez de escribir la expresión completa, a cada condición le asignamos una letra, por ejemplo:

Tabla de verdad (situaciones posibles)
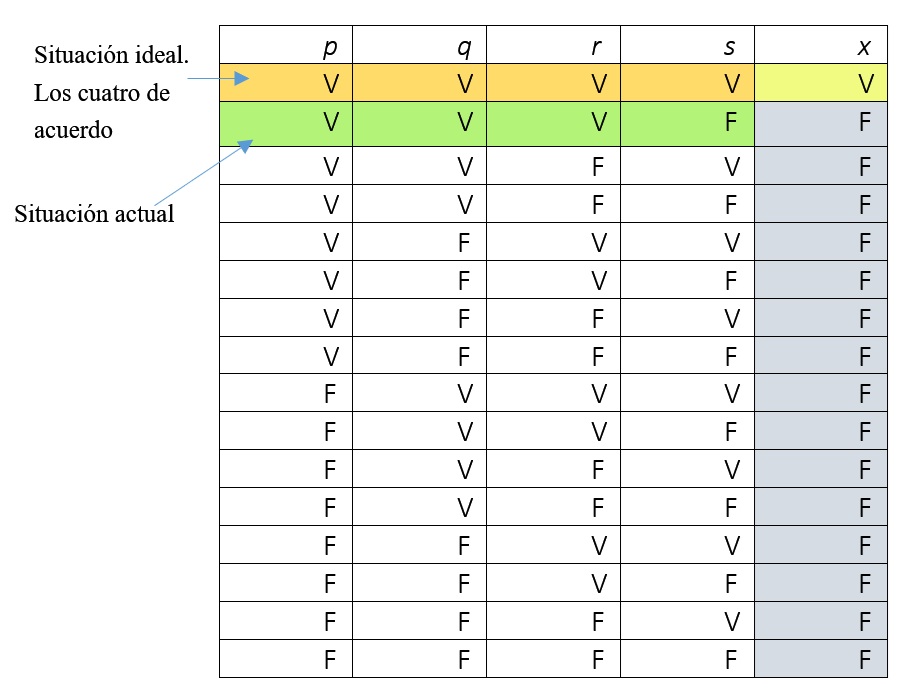
Se mencionaron algunas variables y valores que pueden adoptar.
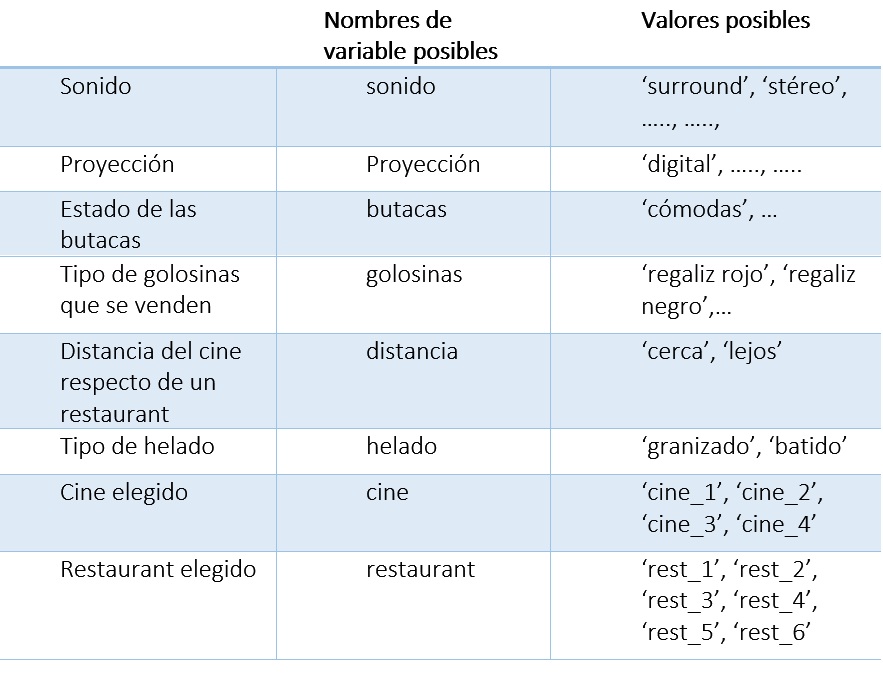
Dadas estas variables, veremos cómo están constituidas las condiciones de cada uno.
Condiciones de Leonard
Leonard se propone encontrar “un restaurant aprobado por Sheldon cerca de un cine aprobado por Sheldon”.
A Leonard le parece bien que los cines tengan sonido surround y la proyección sea digital. Pero no lo expresa como una condición excluyente. Sólo está tratando de conformar a Sheldon.
Por lo tanto, el planteo de Leonard se presenta como una típica disyunción no excluyente. Aunque le parece bien que el sonido sea surround, también aceptaría que fuera stereo. Y respecto de la proyección podría ser digital o no. Sólo está haciendo sugerencias. Podría expresarse de este modo:
SI sonido es surround o si el sonido es estéreo
El cine es aprobado por Leonard
En pseudocódigo:
SI (sonido=’surround’ OR sonido=’stereo’) ENTONCES
Aprobado= V
En una tabla de verdad, la disyunción no excluyente se expresaría así:
dadas las siguientes premisas,
s: sonido = ‘surround’
t: sonido = ‘stereo’
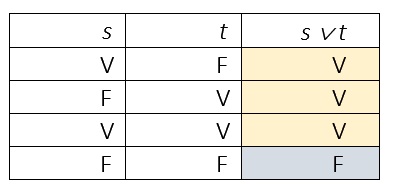
La disyunción no excluyente, se cumple fácilmente, es más probable que se cumpla a que esto no suceda. Este esquema puede observarse en la tabla de verdad, donde aparece tres veces la V y una la F.
Ejercicio 3:
Escribe dos ejemplos de situaciones que expresen una disyunción no excluyente.
La expresión ‘ENTONCES’ permite establecer una regla de inferencia, es decir que si se cumple una afirmación se deduce otra en consecuencia. En este caso, si se cumple la condición del sonido (que no es nada pretensiosa) el cine es aprobado.
s ∨ t ⇒ u
Se lee: s o t implica u. Donde u es (cine=’aprobado’)
Tabla de verdad que expresa la inferencia
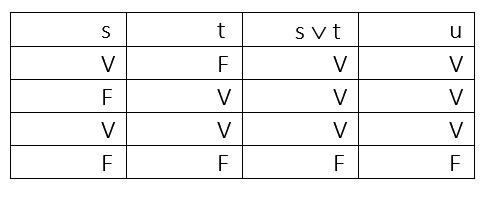
A Leonard también le preocupa que el cine esté cerca de un restaurant porque le gustaría cenar antes de ir al cine. Aunque tampoco parece ser una condición excluyente. ¿Como lo expresarías si fuera una condición excluyente (siendo w: distancia=’cerca’ y z: distancia=’lejos’)?
Ejercicio 4: Condiciones de Rajesh
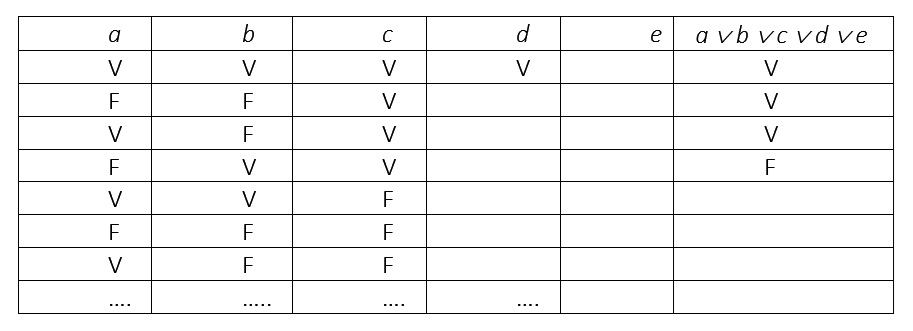
Rajesh descubre que cerca del cine que proyecta a las 7:20, hay un puesto de venta de batidos y lo propone en reemplazo de los granizados de Sheldon, propone que ‘granizado’ no sea condición excluyente. En ese caso, además, podrían elegir entre tres restaurants cercanos que llamaremos ‘rest_1’, ‘rest_2’ y ‘rest_3’. Cualquiera de los tres restaurants tiene el mismo peso para él, es decir, es otra condición disyuntiva no excluyente. Podría expresarse de este modo:

Más formalmente:

En una tabla de verdad, la disyunción no excluyente se expresaría así:
dadas las siguientes premisas,
a: helado=’batido’
b: helado=’granizado’
c: restaurant=’Rest_1’
d: restaurant=’Rest_2’
e: restaurant=’Rest_3’
Tabla de verdad que expresa la inferencia
Ejercicio 5
¿Cómo completarías la tabla? ¿Cuál sería el número total de filas?
¿En cuántos casos se cumple la disyunción no excluyente? ¿En cuántos casos no se cumple?
Condiciones de Sheldon
Sheldon representa la exigencia de la conjunción y la exclusión. Su inflexibilidad da origen al problema, sus condiciones deben cumplirse de un solo modo y no hay lugar a cambios de opinión.
El cine debe vender regalíz negro y no rojo. El restaurant debe ofrecer granizados, que no pueden ser reemplazados por ningún batido.
El restaurant y cine que Sheldon ha aprobado no se encuentran cerca el uno del otro. El horario de la proyección no les permite comer antes de ver la película. Un algoritmo posible es:
SI golosina = ‘regaliz_negro’ AND
helado = ‘batido’ AND
restaurant = ‘rest_4’ AND
cine = ‘cine_3’ AND
distancia = ’cerca’
ENTONCES cine_aprobado = V
En el algoritmo, lo que distingue a estas últimas condiciones de las primeras, es que usan la palabra AND, y es menos probable que se cumplan.
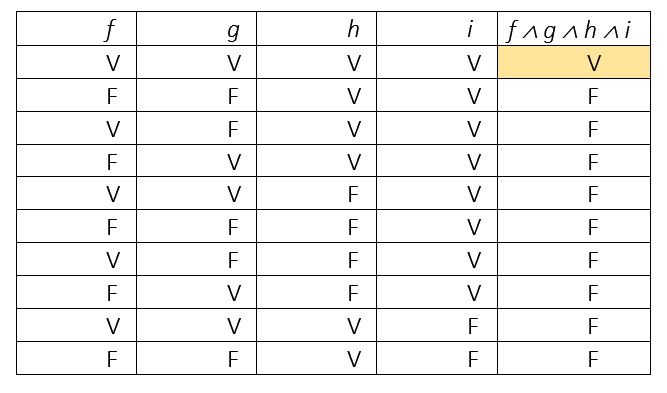
En una tabla de verdad, la conjunción de algunas de las condiciones se expresaría así:
dadas las siguientes premisas,
f: helado=’granizado’
g: golosina=’regaliz negro’
h: restaurant=’rest_4’
i: distancia=’cerca’
Tabla de verdad que expresa la inferencia
Ejercicio 6
- ¿Cómo completarías la tabla agregando otras condiciones?
- ¿Cuál sería el número total de filas?
- ¿En cuántos casos se cumpliría la conjunción?






